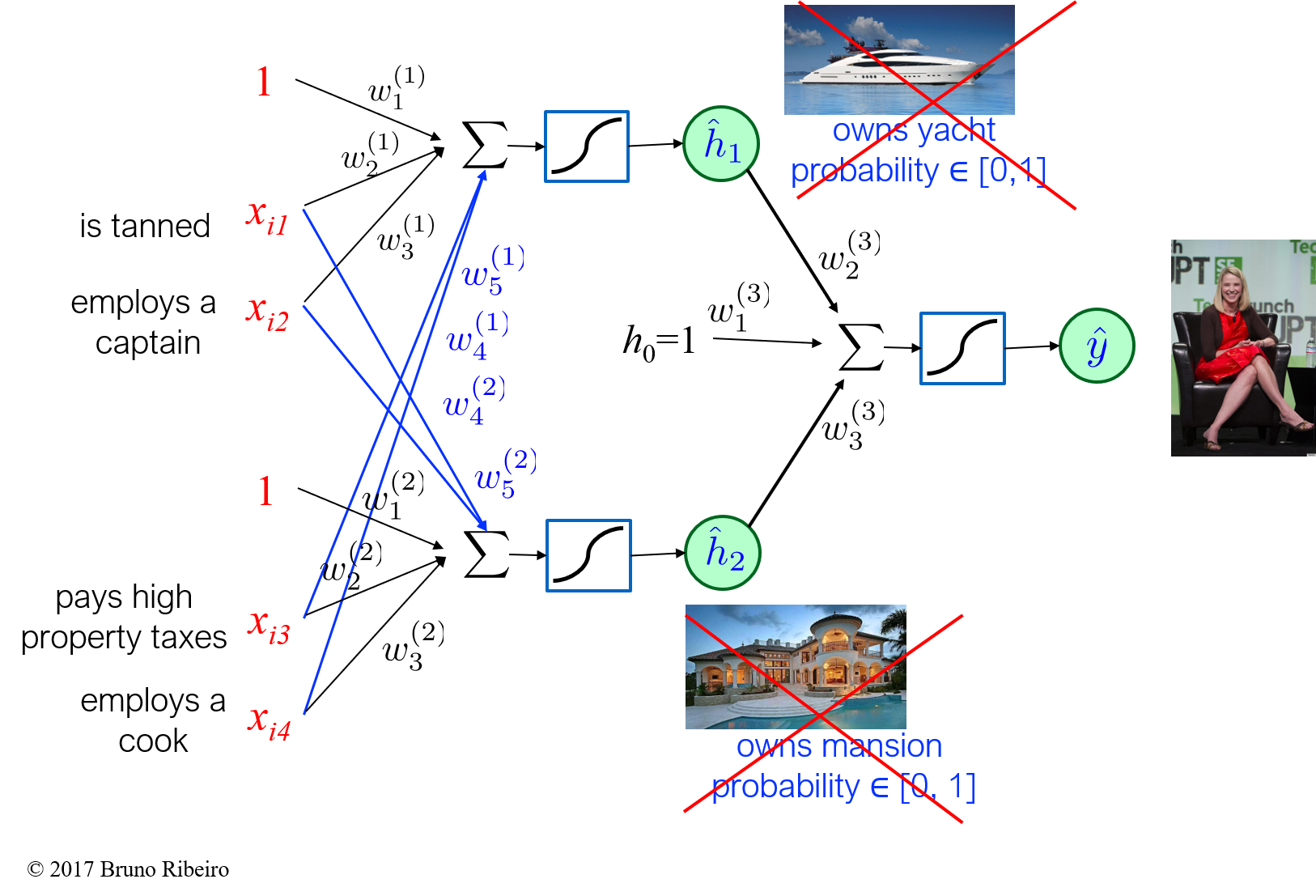
What is Backpropagation?¶
- Backpropagation is an algorithm used for computing gradients of the parameters of a neural network with respect to a loss function.
- It computes the gradient of the loss function with respect to each weight by propagating the error backward through the network, using the chain rule to update the weights in proportion to the error's gradient.
- a univariate (non-polynomial) activation function, denoted $\sigma : \mathbb{R} \to \mathbb{R}$,
- a (column) vector of weights, denoted ${\bf w} = (w_1, \ldots, w_n) \in \mathbb{R}^n$, and
- a threshold (bias) value, denoted $b \in \mathbb{R}$.
Given an input vector ${\bf x} = (x_l, \ldots , x_n)$ is fed into the neuron through the input units, the neuron function computes $h({\bf x}) = \sigma({\bf w}^T {\bf x} + b)$. The value of this function is the neuron's output.
Gradient Descent: General Recursive Gradient Computation (Backpropagation)¶
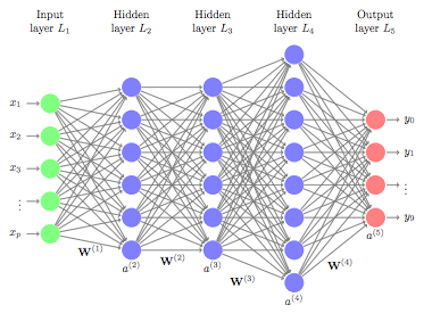
Recap: Feedforward neural network (FFNN a.k.a. MLP)¶
The general architecture of a feedforward neural network is:
- an input layer with $n$ input-units
- an output layer with $m$ outputs
- and one or more hidden layers consisting of intermediate neuron outputs.
- the superscript $(k)$ in the parameters (weights) ${\bf W}^{(k)}$ will indicate they belong to layer $k$
- if layer $k$ has $d_\text{in}$ inputs and $d_\text{out}$ outputs, then the neuron weights ${\bf W}^{(k)}\in \mathbb{R}^{n_\text{in} \times n_\text{out}}$ are a $n_\text{in} \times n_\text{out}$ matrix
The maximum log-likelihood optimization will use gradient ascent:
Let ${\bf W} = ({\bf w}^{(1)},{\bf w}^{(2)},{\bf w}^{(3)})$.
Obtaining ${\bf W}$ via maximum likelihood estimation using gradient ascent.
Let $\text{Data} = \{({\bf x}(i),y(i))\}_{i=1}^n$
$$\begin{align*}
&\frac{\partial}{\partial {\bf W}} \text{log-likelihood(Data)} = \frac{\partial}{\partial {\bf W}} \sum_{i=1}^n \log p(y = y(i) | {\bf x}(i); {\bf w}^{(1)}, {\bf w}^{(2)}, {\bf w}^{(3)} ) \\
&= \sum_{i=1}^n y(i) \frac{\partial}{\partial {\bf W}} \log \sigma(({\bf w}^{(3)})^T {\bf h}({\bf x}(i))) + (1 - y(i)) \frac{\partial}{\partial {\bf W}} \log (1-\sigma(({\bf w}^{(3)})^T {\bf h}({\bf x}(i)))) \\
\end{align*}
$$
where $\sigma(x) = \frac{\exp(x)}{1 + \exp(x)}$, and ${\bf h}({\bf x}) = (1,\hat{h}_1({\bf x}),\hat{h}_2({\bf x}))$,
$$
\hat{h}_1({\bf x}) = p(h_1 = 1 | {\bf x}) = \sigma(({\bf w}^{(1)})^T {\bf x})
$$
and
$$
\hat{h}_2({\bf x}) = p(h_2 = 1 | {\bf x}) = \sigma(({\bf w}^{(2)})^T {\bf x})
$$
How can we compute these gradients? Here, we will resort to the chain rule of vector Calculus.
In a deep neural network each layer is a composition of previous layers, in our previous example the composition looks like:
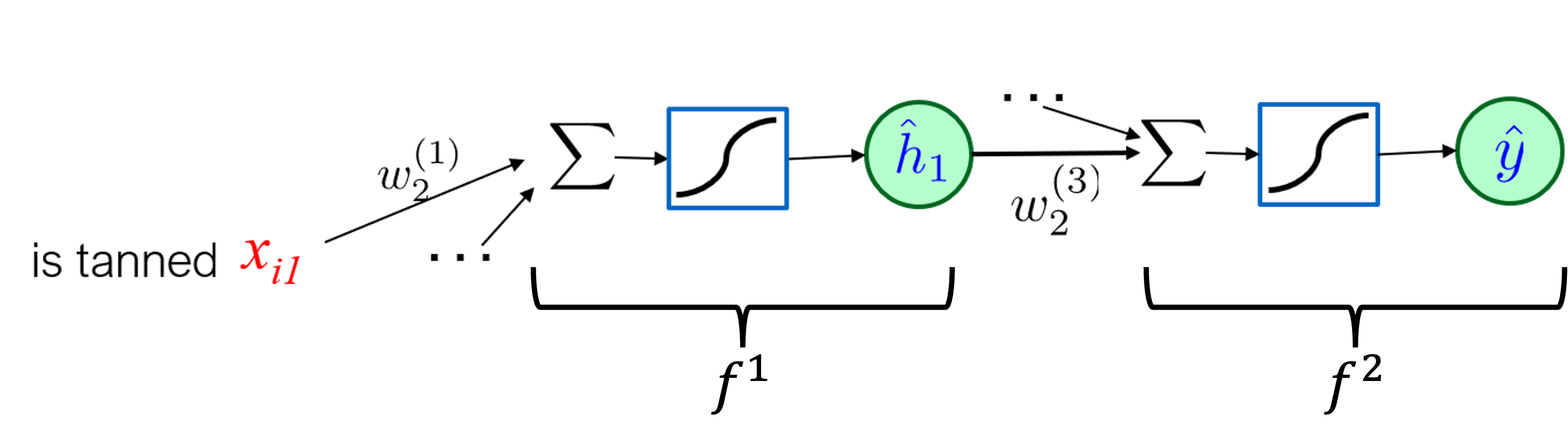 defined as
$$f^1({\bf x};{\bf w}^{(1)}) = \sigma(({\bf w}^{(1)})^T {\bf x}), $$
and
$$f^2({\bf h};{\bf w}^{(3)}) = \sigma(({\bf w}^{(3)})^T {\bf h}) ,$$
where $\hat{{\bf h}} = (1,\hat{h}_1,\hat{h}_2)$.
defined as
$$f^1({\bf x};{\bf w}^{(1)}) = \sigma(({\bf w}^{(1)})^T {\bf x}), $$
and
$$f^2({\bf h};{\bf w}^{(3)}) = \sigma(({\bf w}^{(3)})^T {\bf h}) ,$$
where $\hat{{\bf h}} = (1,\hat{h}_1,\hat{h}_2)$.
The derivative of the composition $f^2(f^1(x;{\bf w}^{(1)});{\bf w}^{(3)})$ with respect to ${\bf w}^{(1)}_2$ is $$ \frac{\partial f^2(f^1(x;{\bf w}^{(1)});{\bf w}^{(3)})}{\partial {\bf w}^{(1)}_2} = \frac{\partial f^2({\bf h})}{\partial {\bf h}} \bigg|_{h = f^1({\bf x};{\bf w}^{(1)})} \cdot \frac{\partial f^1({\bf x};{\bf w}^{(1)})}{\partial {\bf w}_2^{(1)}}. $$
General solution: Consider having $K > 1$ hidden layers. The influence of a lower layer parameter in the final error can be recovered by the chain rule, which generally states:
$$ \frac{\partial f^K(f^{K-1}(\cdots f^2(f^1(x;{\bf w}^{(1)}))\cdots))}{\partial {\bf w}^{(1)}_2} = \frac{\partial f^K(f^{K-1})}{\partial f^{K-1}} \cdot \frac{\partial f^{K-1}(f^{K-2})}{\partial f^{K-2}} \cdots \frac{\partial f^2(f^1)}{\partial f^1} \cdot \frac{\partial f^1({\bf x};{\bf w}^{(1)})}{\partial {\bf w}_2^{(1)}}. $$
General Recursive Gradient Computation (Backpropagation)¶
More generally, for deep neural networks we have no hope of writing down gradient formula for all parameters. We need a recursive method.
- backpropagation = recursive application of the chain rule along a computational graph to compute the gradients of all inputs/parameters/intermediates
- Widely used implementations maintain a graph structure, where the nodes implement the forward() / backward() functions.
- forward pass: compute result of an operation and save any intermediates needed for gradient computation in memory
- backward pass: apply the chain rule to compute the gradient of the loss function with respect to the inputs.
The recursion can be explained with a single image. Consider the following general algorithm to recursively compute the gradient:
- The activations of the hidden neurons are given by $\hat{{\bf h}}^{(k)} = (1,\sigma({\bf W}_k \hat{{\bf h}}^{(k-1)}))$, $k=1,\ldots,K$, where
- The input is $\hat{{\bf h}}^{(0)} = ({\bf x},1)$, where ${\bf x}$ is a single training example.
- And the operator $(1,{\bf z})$ concatenates $1$ to vector ${\bf z}$.
- $L(\hat{{\bf h}}^{(K)})$ is the log-likelihood of a single example. If we consider multiple training examples $\{{\bf x}_1,\ldots,{\bf x}_N\}$, we have the loss over $L(\{\hat{{\bf h}}^{(K)}(i)\}_{i=1}^N)$, which is the sum of the losses over each individual training example.

Backpropagation: Practical Challenges with Deep Models¶
Quiz 1: Understanding backpropagation as an algorithm that is called up to $K$ times, recursively, to multiplies gradients, what can be the practical challenges of performing gradient descent of a deep model ($K \gg 1$)?
We will revisit this question later in the course.
The following code requires Python 3.5 or greater.¶
Example: Feedforward Classification using Python + Numpy¶
In this iPython noteboook we will see how to create a neural network classifier using python and numpy.¶
Part of the code of this notebook uses the incomplete example in [https://wiseodd.github.io/techblog/2016/06/21/nn-sgd/]
First, let's create a simple dataset and split into training and testing.
from sklearn.datasets import make_moons
from sklearn.model_selection import train_test_split
import pylab
import numpy as np
X, y = make_moons(n_samples=5000, random_state=42, noise=0.1)
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=42,test_size=0.3)
Ploting the data...¶
pylab.scatter(X[:,0], X[:,1], c=y)
pylab.show()
Create the Neural Network Weights and Initialize Them¶
We first define:
- the input layer (two coordinates)
- number of hidden layers (we will use one)
- the number of output neurons (number of classes, two in our case)
These are all defined by defining the hidden layer matrices¶
Q1:We have only one hidden layer, how many matrices do we have?
A1: Two matrices, $W_1$ and $W_2$.
A2: One matrix, $W$.
Q2: How do we initialize these matrices?
A1: With zeros.
A2: With ones.
A3: Randomly. We can use a Standard Normal distribution, for instance.
# There are only two features in the data X[:,0] and X[:,1]
n_feature = 2
# There are only two classes: 0 (purple) and 1 (yellow)
n_class = 2
def init_weights(n_hidden=100):
# Initialize weights with Standard Normal random variables
model = dict(
W1=np.random.randn(n_feature + 1, n_hidden),
W2=np.random.randn(n_hidden + 1, n_class)
)
return model
Define the nonlinear activation function (will be used in the last layer)¶
We will use the softmax function.
$$ \text{softmax}(x_i) = \frac{\exp(x_i)}{\sum_j \exp(x_j)} $$
If there are only two classes, the softmax is equivalent to the logistic function (do the math to convince yourself).
Python + Numpy tricks¶
Numpy is very handy. If we give a vector $x$, np.exp($x$) returns a vector with all elements of $x$ exponentiated.
If $y$ is a vector, $y$.sum() returns the sum of the elements in $y$.
# Defines the softmax function. For two classes, this is equivalent to the logistic regression
def softmax(x):
return np.exp(x) / np.exp(x).sum()
Define the forward pass¶
Here, we define how the neural network get an input $x$ and use the model paramters (weights) $W_1$ and $W_2$ and biases $b_1$ and $b_2$ to predict the class labels of the input
Hidden layer activation¶
From the input vector $x$ to the hidden layer neurons $h$, we need to get the intermediate value $$ z_1 = x W_1 + b_1 $$ and pass it through an activation function.
Our activation function is the ReLU: $$ \text{ReLU}(z) = \begin{cases} z & ,\text{if }z \geq 0 \\ 0 & ,\text{if }z < 0 \end{cases} $$ Thus, $$h = \text{ReLU}(z_1).$$
Once we get the hidden layer values $h$, we do $$ z_2 = h W_2 + b_2 $$ and pass it through the activation of the last layer $$ \hat{y} = \text{softmax}(z_2). $$
# For a single example $x$
def forward(x, model):
x = np.append(x, 1)
# Input times first layer matrix
z_1 = x @ model['W1']
# ReLU activation goes to hidden layer
h = z_1
h[z_1 < 0] = 0
# Hidden layer values to output
h = np.append(h, 1)
hat_y = softmax(h @ model['W2'])
return h, hat_y
Define backpropagation¶
Now, we need to backpropagate the derivatives of each example
The backpropagation function gets:
- all input data $\{x_i\}_i$
- corresponding hidden values of all training examples: $\{h_i\}_i$
- errors of each output neuron for all training examples: $\{y_i - \hat{y}_i\}_i$ (this is a subtraction of two vectors)
Our score function of training example $i$ will be, which is the log likelihood of a one-hot enconding vector of the classes,
$$
L(i) = \sum_{j=1}^2 y_i(j) \log \hat{y}_i(j) ,
$$
where $y_i(j)$ is the element $j$ of the vector representing the one-hot enconding of the class of training example $i$ and $\hat{y}_i(j)$ is the output of the $j$-th output neuron for training example $i$,
$$
\hat{y}_i(j) = \frac{\exp(z_2(j))}{\sum_k \exp(z_2(k))}.
$$
The derivative of the loss with respect to $z_2$ will be a vector (that we will represent using the variables without the index $j$)
$$\frac{\partial L(i)}{\partial z_2} = (y_i(1) - \hat{y}_i(1),\ldots,y_i(\text{n\_class}) - \hat{y}_i(\text{n\_class})) = y_i - \hat{y}_i.$$
Note that we can get this derivative directly from the relative error errs.
Other derivatives¶
It will compute the following derivatives for each training example:
- The derivative of the last layer parameters are $$ \frac{\partial L(i)}{\partial W_2} = \frac{\partial z_2(i)}{\partial W_2} \frac{\partial L(i)}{\partial z_2} = h_i^T (y_i - \hat{y}_i) $$ and $$ \frac{\partial L(i)}{\partial b_2} = \frac{\partial z_2(i)}{\partial b_2} \frac{\partial L(i)}{\partial z_2} = (y_i - \hat{y}_i), $$ as $$ \frac{\partial z_2(i)}{\partial b_2} = 1. $$
- The derivatives with respect to the hidden values of the previous layer are $$ \frac{\partial L(i)}{\partial h} = \frac{\partial z_2(i)}{\partial h} \frac{\partial L(i)}{\partial z_2} = W_2 (y_i - \hat{y}_i) $$
We then backpropagate $\partial L(i)/\partial h $ to the previous layer. This will be needed in the final derivative the final derivatives are $$ \frac{\partial L(i)}{\partial W_1} = \frac{\partial z_1(i)}{\partial W_1} \frac{\partial h(i)}{\partial z_1} \frac{\partial L(i)}{\partial h}, $$ and $$ \frac{\partial L(i)}{\partial b_1} = \frac{\partial z_1(i)}{\partial b_1} \frac{\partial h(i)}{\partial z_1} \frac{\partial L(i)}{\partial h}, $$
where $$ \frac{\partial z_1(i)}{\partial W_1} = x_i, $$ and $$ \frac{\partial z_1(i)}{\partial b_1} = 1, $$ and the derivative of the ReLU $$ \frac{\partial h(i)}{\partial z_1} = \begin{cases} 1 &, \text{if }z_1(i) > 0\\ 0 & \text{otherwise}. \end{cases}. $$
The final output are the derivatives of the parameters.
In the above, we have described the backpropagation algorithm per training example. The following python code will, as described earlier, give all examples as inputs. Thus, the input is a matrix whose rows are the vectors of each training example.
This function outputs $$ \text{d}W_1 = \sum_{i=1}^N \frac{\partial L(i)}{\partial W_1}, $$ $$ \text{d}b_1 = \sum_{i=1}^N \frac{\partial L(i)}{\partial b_1}, $$ $$ \text{d}W_2 = \sum_{i=1}^N \frac{\partial L(i)}{\partial W_2}, $$ and $$ \text{d}b_2 = \sum_{i=1}^N \frac{\partial L(i)}{\partial b_2}. $$
def backward(model, xs, hs, errs):
"""xs, hs, errs contain all information (input, hidden state, error) of all data in the minibatch"""
# errs is the gradients of output layer for the minibatch
dW2 = (hs.T @ errs)/xs.shape[0]
# Get gradient of hidden layer
dh = errs @ model['W2'].T
dh[hs <= 0] = 0
# The bias "neuron" is the constant 1, we don't need to backpropagate its gradient
# since it has no inputs, so we just remove its column from the gradient
dh = dh[:, :-1]
# Add the 1 to the data, to compute the gradient of W1
xs = np.hstack([xs, np.ones((xs.shape[0], 1))])
dW1 = (xs.T @ dh)/xs.shape[0]
return dict(W1=dW1, W2=dW2)
Do the forward and backward procedures to get the gradient¶
For each input example $i$ in the training data, perform a forward pass and:
- store all the hidden units of all the hidden layers associated with example $i$ (we only have to store one vector of hidden values)
- store the gradient of the error of example $i$ with respect to the prediction
Once we have store all hidden layer values and all the derivatives of all examples, we will do the backard pass and return the derivatives of the error with respect to the paramters $W_1$, $b_1$, $W_2$, and $b_2$.
def get_gradient(model, X_train, y_train):
xs, hs, errs = [], [], []
for x, cls_idx in zip(X_train, y_train):
h, y_pred = forward(x, model)
# Create one-hot coding of true label
y_true = np.zeros(n_class)
y_true[int(cls_idx)] = 1.
# Compute the gradient of output layer
err = y_true - y_pred
# Accumulate the informations of the examples
# x: input
# h: hidden state
# err: gradient of output layer
xs.append(x)
hs.append(h)
errs.append(err)
# Backprop using the informations we get from the current minibatch
return backward(model, np.array(xs), np.array(hs), np.array(errs))
One gradient ascent step¶
Perform a single gradient ascent step.
Get the gradients and perform the following updates for $N$ training examples: $$ W_1 =W_1 + \epsilon \frac{1}{N} \sum_{i=1}^N \frac{\partial L(i)}{\partial W_1}, $$ $$ b_1 =b_1 + \epsilon \frac{1}{N} \sum_{i=1}^N \frac{\partial L(i)}{\partial b_1}, $$ $$ W_2 =W_2 + \epsilon \frac{1}{N} \sum_{i=1}^N \frac{\partial L(i)}{\partial W_2}, $$ and $$ b_2 =b_2 + \epsilon \frac{1}{N} \sum_{i=1}^N \frac{\partial L(i)}{\partial b_2}, $$ where $\epsilon = 10^{-1}$ in our example.
def gradient_step(model, X_train, y_train, learning_rate=1e-1):
grad = get_gradient(model, X_train, y_train)
model = model.copy()
# Update every parameters in our networks (W1 and W2) using their gradients
for layer in grad:
# Learning rate: 1e-1
model[layer] += learning_rate * grad[layer]
return model
Do gradient ascent some fixed number of times¶
def gradient_ascent(model, X_train, y_train, no_iter=10):
for iter in range(no_iter):
print('Iteration {}'.format(iter))
model = gradient_step(model, X_train, y_train)
return model
Train the model and test the accuracy over the test data¶
We now train the model and output the prediction error over the test data.
Note that the output has two neurons for the two classes. Our prediction will chose the class corresponding to the largest output neuron value.
no_iter = 200
# Reset model
model = init_weights()
# Train the model
model = gradient_ascent(model, X_train, y_train, no_iter=no_iter)
y_pred = np.zeros_like(y_test)
accuracy = 0
for i, x in enumerate(X_test):
# Predict the distribution of label
_, prob = forward(x, model)
# Get label by picking the most probable one
y = np.argmax(prob)
y_pred[i] = y
# Accuracy of predictions with the true labels and take the percentage
# Because our dataset is balanced, measuring just the accuracy is OK
accuracy = (y_pred == y_test).sum() / y_test.size
print('Accuracy after {} iterations: {}'.format(no_iter,accuracy))
Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Iteration 10 Iteration 11 Iteration 12 Iteration 13 Iteration 14 Iteration 15 Iteration 16 Iteration 17 Iteration 18 Iteration 19 Iteration 20 Iteration 21 Iteration 22 Iteration 23 Iteration 24 Iteration 25 Iteration 26 Iteration 27 Iteration 28 Iteration 29 Iteration 30 Iteration 31 Iteration 32 Iteration 33 Iteration 34 Iteration 35 Iteration 36 Iteration 37 Iteration 38 Iteration 39 Iteration 40 Iteration 41 Iteration 42 Iteration 43 Iteration 44 Iteration 45 Iteration 46 Iteration 47 Iteration 48 Iteration 49 Iteration 50 Iteration 51 Iteration 52 Iteration 53 Iteration 54 Iteration 55 Iteration 56 Iteration 57 Iteration 58 Iteration 59 Iteration 60 Iteration 61 Iteration 62 Iteration 63 Iteration 64 Iteration 65 Iteration 66 Iteration 67 Iteration 68 Iteration 69 Iteration 70 Iteration 71 Iteration 72 Iteration 73 Iteration 74 Iteration 75 Iteration 76 Iteration 77 Iteration 78 Iteration 79 Iteration 80 Iteration 81 Iteration 82 Iteration 83 Iteration 84 Iteration 85 Iteration 86 Iteration 87 Iteration 88 Iteration 89 Iteration 90 Iteration 91 Iteration 92 Iteration 93 Iteration 94 Iteration 95 Iteration 96 Iteration 97 Iteration 98 Iteration 99 Iteration 100 Iteration 101 Iteration 102 Iteration 103 Iteration 104 Iteration 105 Iteration 106 Iteration 107 Iteration 108 Iteration 109 Iteration 110 Iteration 111 Iteration 112 Iteration 113 Iteration 114 Iteration 115 Iteration 116 Iteration 117 Iteration 118 Iteration 119 Iteration 120 Iteration 121 Iteration 122 Iteration 123 Iteration 124 Iteration 125 Iteration 126 Iteration 127 Iteration 128 Iteration 129 Iteration 130 Iteration 131 Iteration 132 Iteration 133 Iteration 134 Iteration 135 Iteration 136 Iteration 137 Iteration 138 Iteration 139 Iteration 140 Iteration 141 Iteration 142 Iteration 143 Iteration 144 Iteration 145 Iteration 146 Iteration 147 Iteration 148 Iteration 149 Iteration 150 Iteration 151 Iteration 152 Iteration 153 Iteration 154 Iteration 155 Iteration 156 Iteration 157 Iteration 158 Iteration 159 Iteration 160 Iteration 161 Iteration 162 Iteration 163 Iteration 164 Iteration 165 Iteration 166 Iteration 167 Iteration 168 Iteration 169 Iteration 170 Iteration 171 Iteration 172 Iteration 173 Iteration 174 Iteration 175 Iteration 176 Iteration 177 Iteration 178 Iteration 179 Iteration 180 Iteration 181 Iteration 182 Iteration 183 Iteration 184 Iteration 185 Iteration 186 Iteration 187 Iteration 188 Iteration 189 Iteration 190 Iteration 191 Iteration 192 Iteration 193 Iteration 194 Iteration 195 Iteration 196 Iteration 197 Iteration 198 Iteration 199 Accuracy after 200 iterations: 0.99
pylab.scatter(X_test[:,0], X_test[:,1], c=y_pred)
pylab.show()
no_iter = 10
no_runs = 10
accuracies = np.zeros(no_runs)
for run in range(no_runs):
print("Run {}".format(run))
# Reset model
model = init_weights()
# Train the model
model = gradient_ascent(model, X_train, y_train, no_iter=no_iter)
y_pred = np.zeros_like(y_test)
for i, x in enumerate(X_test):
# Predict the distribution of label
_, prob = forward(x, model)
# Get label by picking the most probable one
y = np.argmax(prob)
y_pred[i] = y
# Accuracy of predictions with the true labels and take the percentage
# Because our dataset is balanced, measuring just the accuracy is OK
accuracies[run]= (y_pred == y_test).sum() / y_test.size
print('Mean accuracy over test data: {}, std: {}'.format(accuracies.mean(), accuracies.std()))
Run 0 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Run 1 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Run 2 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Run 3 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Run 4 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Run 5 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Run 6 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Run 7 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Run 8 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Run 9 Iteration 0 Iteration 1 Iteration 2 Iteration 3 Iteration 4 Iteration 5 Iteration 6 Iteration 7 Iteration 8 Iteration 9 Mean accuracy over test data: 0.8674666666666667, std: 0.045322351611049