Books and Surveys
|
|
|
Delaunay Mesh Generation.
Siu-Wing
Cheng, Tamal K. Dey, Jonathan R. Shewchuk. Published
by CRC Press (2012 December). Details and Sample
Chapters including a new algorithm for meshing 3D polyhedra with arbitrary
small angles (chapter 9).
Order
link
| 
|
|
|
|
Delaunay
mesh generation of three dimensional
domains.
T. K. Dey. Technical Report
OSU-CISRC-9/07-TR64, October, 2007.
To appear in Tessellations in the sciences:
Virtues, Techniques and Applications of Geometric Tilings,
eds. R. van de Weygaert, G. Vegter, J. Ritzerveld & V.
Icke, Springer-Verlag, 2009.
Delaunay meshes are used in various applications such
as finite element analysis, computer graphics rendering,
geometric modeling, and shape analysis. As the
applications vary, so do the domains to be meshed. Although
meshing of geometric domains with Delaunay simplices
have been around for a while, provable techniques to meshing
various types of three dimenisonal domains have been developed
only recently. We devote this article to presenting these
techniques. We survey various related results and detail a
few core algorithms that have provable guarantees and are amenable
to practical implementation. Delaunay refinement, a paradigm
originally developed for guaranteeing shape quality of mesh
elements, is a common thread in these algorithms. We finish
the article by listing a set of open questions.
|

|
|
|
|
Sample
based geometric
modeling
T. K. Dey.
Chapter in Geometric and Algorithmic
Aspects of Computer-Aided Design and Manufacturing,
eds Janardan, Smid, Dutta. DIMACS series
in Discrete Mathematics and Theoretical Computer Science,
Volume 67, 2005.
A new paradigm for
digital modeling of physical objects from
sample points is fast emerging due to recent
advances in scanning technology. Researchers
are investigating many of the traditional
modeling problems in this new setting. We name this
new area as sample based geometric
modeling. The purpose
of this article is to expose the readers to this
new modeling paradigm through three basic problems,
namely surface reconstruction, medial axis approximation,
and shape segmentation. The algorithms for
these three problems developed by the author and his
co-authors are described. |

|
|
Curve
and surface reconstruction
T. K. Dey.
Chapter in Handbook of Discrete
and Computational Geometry, Goodman and O'
Rourke eds., CRC press, 2nd edition (2004)
New version for 3rd edition published (2016).
The problem of reconstructing
a shape from its sample appears in many
scientific and engineering applications.
Because of the variety in shapes and applications,
many algorithms have been proposed over
the last two decades, some of which exploit
application-specific information and some
of which are more general. We will concentrate
on techniques that apply to the general setting and have
proved to provide some guarantees on the quality
of reconstruction. |

|
|
Papers
|
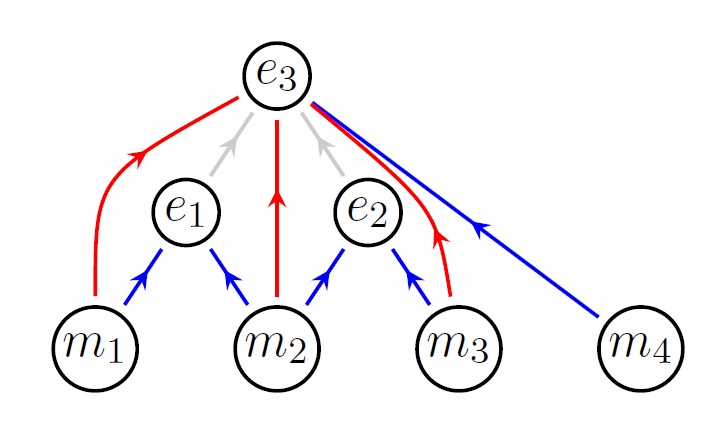
 Limit computation over posets via minimal initial functors Limit computation over posets via minimal initial functors
T. K. Dey, M. Lesnick. https://arxiv.org/abs/2601.00209(2026)
It is
well known that limits can be computed by restricting along an initial
functor, and that this can often simplify limit computation. We
systematically study the algorithmic implications of this idea for
diagrams indexed by a finite poset. We say an initial functor 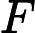    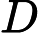 F:C->D with F:C->D with  C small is \emph{minimal} if the sets of objects and morphisms of C small is \emph{minimal} if the sets of objects and morphisms of  C each have minimum cardinality, among the sources of all initial functors with target C each have minimum cardinality, among the sources of all initial functors with target 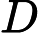 D. For Q D. For Q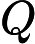 a finite poset or a finite poset or 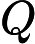 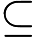   Q\subseteq N^d an interval (i.e., a convex, connected subposet), we describe all minimal initial functors Q\subseteq N^d an interval (i.e., a convex, connected subposet), we describe all minimal initial functors 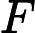  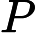  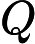 F:P->Q and in particular, show that F:P->Q and in particular, show that 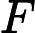 F is always a poset inclusion. We give efficient algorithms to compute a choice of minimal initial functor. In the case that F is always a poset inclusion. We give efficient algorithms to compute a choice of minimal initial functor. In the case that 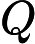 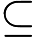   Q\subseteq N^d is an interval, we give asymptotically optimal bounds on |P| Q\subseteq N^d is an interval, we give asymptotically optimal bounds on |P| 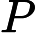  , the number of relations in , the number of relations in 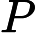 P (including identities), in terms of the number n P (including identities), in terms of the number n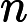 of minima of Q of minima of Q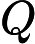 : We show that : We show that 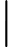 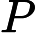 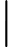    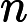  |P|=\Theta(n) for |P|=\Theta(n) for 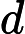 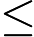 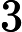 d\leq 3, and d\leq 3, and 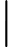 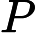 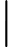    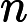   \Theta(n^2) for d>3 \Theta(n^2) for d>3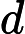  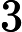 . We apply these results to give new bounds on the cost of computing lim G . We apply these results to give new bounds on the cost of computing lim G 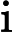 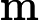 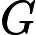 for a functor for a functor 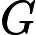  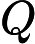  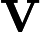  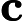 G:Q->Vec valued in vector spaces. For G:Q->Vec valued in vector spaces. For 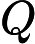 Q connected, we also give new bounds on the cost of computing the \emph{generalized rank} of G Q connected, we also give new bounds on the cost of computing the \emph{generalized rank} of G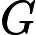 (i.e., the rank of the induced map lim G->colim G (i.e., the rank of the induced map lim G->colim G  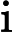 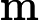 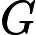  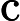      ), which is of interest in topological data analysis. ), which is of interest in topological data analysis.
|
|
|
 Fast free resolutions of bifiltered chain complexes Fast free resolutions of bifiltered chain complexes
U. Bauer, T. K. Dey, M. Kerber, F. Russo, and M. Sols. to appear Proc. 42nd Internat. Sympos. Comput. Geom. (SoCG 2026), https://arxiv.org/abs/2512.08652
In a  k-critical bifiltration, every simplex enters along a staircase with at most k-critical bifiltration, every simplex enters along a staircase with at most  k steps. Examples with k steps. Examples with    k>1 include degree-Rips bifiltrations and models of the multicover bifiltration. We consider the problem of converting a k>1 include degree-Rips bifiltrations and models of the multicover bifiltration. We consider the problem of converting a  k-critical bifiltration into a k-critical bifiltration into a  1-critical
(i.e. free) chain complex with equivalent homology. This is known as
computing a free resolution of the underlying chain complex and is a
first step toward post-processing such bifiltrations. We
present two algorithms. The first one computes free resolutions
corresponding to path graphs and assembles them to a chain complex by
computing additional maps. The simple combinatorial structure of path
graphs leads to good performance in practice, as demonstrated by
extensive experiments. However, its worst-case bound is quadratic in
the input size because long paths might yield dense boundary matrices
in the output. Our second algorithm replaces the simplex-wise path
graphs with ones that maintain short paths which leads to almost linear
runtime and output size. We demonstrate that pre-computing a free resolution speeds up the task of computing a minimal presentation of the homology of a 1-critical
(i.e. free) chain complex with equivalent homology. This is known as
computing a free resolution of the underlying chain complex and is a
first step toward post-processing such bifiltrations. We
present two algorithms. The first one computes free resolutions
corresponding to path graphs and assembles them to a chain complex by
computing additional maps. The simple combinatorial structure of path
graphs leads to good performance in practice, as demonstrated by
extensive experiments. However, its worst-case bound is quadratic in
the input size because long paths might yield dense boundary matrices
in the output. Our second algorithm replaces the simplex-wise path
graphs with ones that maintain short paths which leads to almost linear
runtime and output size. We demonstrate that pre-computing a free resolution speeds up the task of computing a minimal presentation of the homology of a  k-critical
bifiltration in a fixed dimension. Furthermore, our findings show that
a chain complex that is minimal in terms of generators can be
asymptotically larger than the non-minimal output complex of our second
algorithm in terms of description size. k-critical
bifiltration in a fixed dimension. Furthermore, our findings show that
a chain complex that is minimal in terms of generators can be
asymptotically larger than the non-minimal output complex of our second
algorithm in terms of description size.
|
|
|
 D-Gril: End-to-end topological learning with 2-parameter persistence D-Gril: End-to-end topological learning with 2-parameter persistence
S. Mukherjee, S. N. Samaga, C. Xin, S. Oudot, T. K. Dey. to appear Proc. 42nd Internat. Sympos. Comput. Geom. (SoCG 2026), arXiv:2406.07100
End-to-end
topological learning using 1-parameter persistence is well-known. We
show that the framework can be enhanced using 2-parameter persistence
by adopting a recently introduced 2-parameter persistence based
vectorization technique called GRIL. We establish a theoretical
foundation of differentiating GRIL producing D-GRIL. We show that
D-GRIL can be used to learn a bifiltration function on standard
benchmark graph datasets. Further, we exhibit that this framework can
be applied in the context of bio-activity prediction in drug discovery
|
|
|
 Halluzig: Hallucination detection by zigzag persistence Halluzig: Hallucination detection by zigzag persistence
S. N. Samaga, G. Gonzalez-Arryo, T. K. Dey. to appear in EACL (Oral) (2026), https://arxiv.org/abs/2601.01552 (2026)
The
factual reliability of Large Language Models (LLMs) remains a critical
barrier to their adoption in high-stakes domains due to their
propensity to hallucinate. Current detection methods often rely on
surface-level signals from the model's output, overlooking the failures
that occur within the model's internal reasoning process. In this
paper, we introduce a new paradigm for hallucination detection by
analyzing the dynamic topology of the evolution of model's layer-wise
attention. We model the sequence of attention matrices as a zigzag
graph filtration and use zigzag persistence, a tool from Topological
Data Analysis, to extract a topological signature. Our core hypothesis
is that factual and hallucinated generations exhibit distinct
topological signatures. We validate our framework, HalluZig, on
multiple benchmarks, demonstrating that it outperforms strong
baselines. Furthermore, our analysis reveals that these topological
signatures are generalizable across different models and hallucination
detection is possible only using structural signatures from partial
network depth.
|
|
|
 Conley-Morse persistence barcode: a homological signature of a combinatorial bifurcation Conley-Morse persistence barcode: a homological signature of a combinatorial bifurcation
T. K. Dey, M. Lipinski, M. Soriano-Trigueros. https://arxiv.org/abs/2504.17105(2025)
Bifurcation
is one of the major topics in the theory of dynamical systems. It
characterizes the nature of qualitative changes in parametrized
dynamical systems. In this work, we study combinatorial bifurcations
within the framework of combinatorial multivector field theory--a young
but already well-established theory providing a combinatorial model for
continuous-time dynamical systems (or simply, flows). We introduce
Conley-Morse persistence barcode, a compact algebraic descriptor of
combinatorial bifurcations. The barcode captures structural changes in
a dynamical system at the level of Morse decompositions and provides a
characterization of the nature of observed transitions in terms of the
Conley index. The construction of Conley-Morse persistence barcode
builds upon ideas from topological data analysis (TDA). Specifically,
we consider a persistence module obtained from a zigzag filtration of
topological pairs (formed by index pairs defining the Conley index)
over a poset. Using gentle algebras, we prove that this module
decomposes into simple intervals (bars) and compute them with
algorithms from TDA known for processing zigzag filtrations.
|
|
|
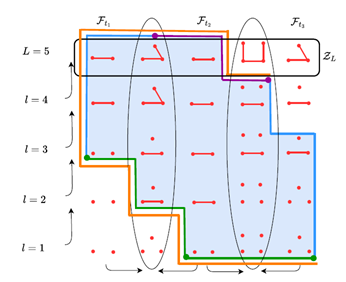
 Computing Projective Implicit Representations from Poset Towers Computing Projective Implicit Representations from Poset Towers
T. K. Dey and F. Russold. https://arxiv.org/abs/2505.08755 (2025)
A family of simplicial complexes, connected with simplicial maps and indexed by a poset P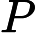 ,
is called a poset tower. The concept of poset towers subsumes classical
objects of study in the persistence literature, as, for example,
one-critical multi-filtrations and zigzag filtrations, but also allows
multi-critical simplices and arbitrary simplicial maps. The homology of
a poset tower gives rise to a P ,
is called a poset tower. The concept of poset towers subsumes classical
objects of study in the persistence literature, as, for example,
one-critical multi-filtrations and zigzag filtrations, but also allows
multi-critical simplices and arbitrary simplicial maps. The homology of
a poset tower gives rise to a P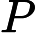 -persistence module. To compute this homology globally over -persistence module. To compute this homology globally over 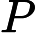 P, in the spirit of the persistence algorithm, we consider the homology of a chain complex of P, in the spirit of the persistence algorithm, we consider the homology of a chain complex of 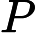 P-persistence modules, C_{l-1}<--C_l<--C_{l+1} P-persistence modules, C_{l-1}<--C_l<--C_{l+1} 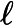         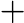  , induced by the simplices of the poset tower. Contrary to the case of one-critical filtrations, the chain-modules C_l , induced by the simplices of the poset tower. Contrary to the case of one-critical filtrations, the chain-modules C_l  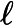 of
a poset tower can have a complicated structure. In this work, we tackle
the problem of computing a representation of such a chain complex
segment by projective modules and of
a poset tower can have a complicated structure. In this work, we tackle
the problem of computing a representation of such a chain complex
segment by projective modules and  P-graded
matrices, which we call a projective implicit representation (PiRep).
We give efficient algorithms to compute asymptotically minimal
projective resolutions (up to the second term) of the chain modules and
the boundary maps and compute a PiRep from these resolutions. Our
algorithms are tailored to the chain complexes and resolutions coming
from poset towers and take advantage of their special structure. In the
context of poset towers, they are fully general and could potentially
serve as a foundation for developing more efficient algorithms on
specific posets. P-graded
matrices, which we call a projective implicit representation (PiRep).
We give efficient algorithms to compute asymptotically minimal
projective resolutions (up to the second term) of the chain modules and
the boundary maps and compute a PiRep from these resolutions. Our
algorithms are tailored to the chain complexes and resolutions coming
from poset towers and take advantage of their special structure. In the
context of poset towers, they are fully general and could potentially
serve as a foundation for developing more efficient algorithms on
specific posets.
|
|
|
 Computing connection matrix and persistence efficiently for a Morse decomposition Computing connection matrix and persistence efficiently for a Morse decomposition
T. K. Dey, A. Haas, M. Lipinski. SIAM J. Applied Dynamical Systems, Vol. 25 (1), pp. 108-130 (2026) https://arxiv.org/abs/2502.19369 (2025)
Morse
decompositions partition the flows in a vector field into equivalent
structures. Given such a decomposition, one can define a further
summary of its flow structure by what is called a connection matrix.
These
matrices, a generalization of Morse boundary operators from classical
Morse theory, capture the connections made by the flows among the
critical structures - such as attractors, repellers, and orbits - in a
vector field. Recently, in the context of combinatorial dynamics, an
efficient persistence-like algorithm to compute connection matrices has
been proposed in~\cite{DLMS24}. We show that, actually, the classical
persistence algorithm with exhaustive reduction retrieves connection
matrices, both simplifying the algorithm of~\cite{DLMS24} and bringing
the theory of persistence closer to combinatorial dynamical systems. We
supplement this main result with an observation: the concept of
persistence as defined for scalar fields naturally adapts to Morse
decompositions whose Morse sets are filtered with a Lyapunov function.
We conclude by presenting preliminary experimental results.
|
|
|
 Quasi Zigzag Persistence: A Topological Framework for Analyzing Time-Varying Data Quasi Zigzag Persistence: A Topological Framework for Analyzing Time-Varying Data
T. K. Dey, S. Samaga. Spotlight paper in TAG-DS, to appear in PMLR. ArXiv https://arxiv.org/abs/2502.16049v1. (2025)
In
this paper, we propose Quasi Zigzag Persistent Homology (QZPH) as a
framework for analyzing time-varying data by integrating multiparameter
persistence and zigzag persistence. To this end, we introduce a stable
topological invariant that captures both static and dynamic features at
different scales. We present an algorithm to compute this invariant
efficiently. We show that it enhances the machine learning models when
applied to tasks such as sleep-stage detection, demonstrating its
effectiveness in capturing the evolving patterns in time-evolving
datasets.
Talk Slides
|
|
|
Decomposing multiparameter persistence modules
T. K. Dey, J. Jendrysiak, and M. Kerber. Proc. 41st Internat. Sympos. Comput. Geom. (SoCG 2025).
Dey and Xin (J.Appl.Comput.Top., 2022) describe an algorithm to
decompose finitely presented multiparameter persistence modules using a
matrix reduction algorithm. Their algorithm only works for modules
whose generators and relations are distinctly graded. We extend their
approach to work on \emph{all} finitely presented modules and introduce
several improvements that lead to significant speed-ups in practice.
Our algorithm is FPT with respect to the maximal number of relations
with the same degree and with further optimisation we obtain an
$O(n^3)$ algorithm for interval-decomposable modules. In particular, we
can decide interval-decomposability in this time. As a by-product to
the proofs of correctness we develop a theory of parameter restriction
for persistence modules. Our algorithm is implemented as a software
library \textsc{aida} which is the first to enable the decomposition of
large inputs. We show its capabilities via extensive experimental
evaluation.
|
|
|
Apex representatives
T. K. Dey, T. Hou and D. Morozov. Proc. 41st Internat. Sympos. Comput. Geom. (SoCG 2025).
Given
a zigzag filtration, we want to find its barcode representatives, i.e.,
a compatible choice of bases for the homology groups that diagonalize
the linear maps in the zigzag. To achieve this, we convert the
input zigzag to a levelset zigzag of a real-valued function. This
function generates a Mayer--Vietoris pyramid of spaces, which generates
an infinite strip of homology groups. We call the origins of
indecomposable (diamond) summands of this strip their apexes and give
an algorithm to find representative cycles in these apexes from
ordinary persistence computation. The resulting representatives map
back to the levelset zigzag and thus yield barcode representatives for
the input zigzag. Our algorithm for lifting a $p$-dimensional cycle
from ordinary persistence to an apex representative
takes $O(p \cdot m \log m)$ time. From this we can recover zigzag
representatives in time $O(\log m + C)$, where $C$ is the size of the
output.
|
|
|
A fast algorithm for computing zigzag representatives
T. K. Dey, T. Hou and D. Morozov. Proc. ACM-SIAM Sympos. Discrete Algorithms (SODA 2025).
Zigzag filtrations of simplicial complexes generalize the usual
filtrations by allowing simplex deletions in addition to simplex
insertions. The barcodes computed from zigzag filtrations encode the
evolution of homological features. Althouhg one can locate a particular
feature at any index in the filtration using existing algorithms, the
resulting representatives may not be compatible with the zigzag: a
representative cycle at one one index may not map into a representative
cycle at its neighbor. For this, one needs to compute compatible
representative cycles along each bar in the barcode. Even thouhg it is
known that the barcode for a zigzag filtration with m insertions and
deletions can be computed in O(m^w) time, it is not known how to
compute the compatible representatuves so efficiently. For a non-zigzag
filtration, the classical matrix-based algorithm provides
representatives in O(m^3) time, which can be improved to O(m^w).
However, no known algorithm for zigzag filtrations computes the
representatives with the O(m^3) time bound. We present an O(m^2n) time
algorithm for this problem, where n\neq m is the size of the largest
complex in the filtratiom.
|

|
|
Computing generalized ranks of persistence modules via unfolding to zigzag modules
T. K. Dey, C. Xin. ArXiv arxiv.org/abs/2403.08110 (2024).
For a 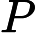 P-indexed persistence module M P-indexed persistence module M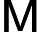 , the (generalized) rank of , the (generalized) rank of 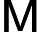 M is defined as the rank of the limit-to-colimit map for the diagram of vector spaces of M is defined as the rank of the limit-to-colimit map for the diagram of vector spaces of 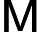 M over the poset M over the poset 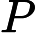 P. For 2 P. For 2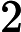 -parameter
persistence modules, recently a zigzag persistence based algorithm has
been proposed that takes advantage of the fact that generalized rank for 2 -parameter
persistence modules, recently a zigzag persistence based algorithm has
been proposed that takes advantage of the fact that generalized rank for 2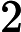 -parameter
modules is equal to the number of full intervals in a zigzag module
defined on the boundary of the poset. Analogous definition of boundary
for d -parameter
modules is equal to the number of full intervals in a zigzag module
defined on the boundary of the poset. Analogous definition of boundary
for d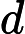 -parameter persistence modules or general -parameter persistence modules or general 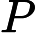 P-indexed persistence modules does not seem plausible. To overcome this difficulty, we first unfold a given P P-indexed persistence modules does not seem plausible. To overcome this difficulty, we first unfold a given P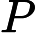 -indexed module -indexed module 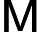 into a zigzag module into a zigzag module 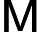 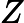 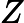 M_ZZ and then check how many full interval modules in a decomposition of M_ZZ and then check how many full interval modules in a decomposition of 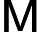 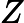 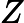 M_ZZ can be folded back to remain full in a decomposition of M M_ZZ can be folded back to remain full in a decomposition of M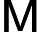 . This number determines the generalized rank of M . This number determines the generalized rank of M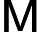 . For special cases of degree- . For special cases of degree-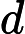 d homology for d d homology for d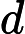 -complexes, we obtain a more efficient algorithm including a linear time algorithm for degree- -complexes, we obtain a more efficient algorithm including a linear time algorithm for degree- 1 homology in graphs. 1 homology in graphs.
|

|
|
Efficient algorithms for computing complexes of persistence modules with applications
T. K. Dey, S. Samaga, F. Russold. Proc. 40th Internat. Sympos. Comput. Geom. (SoCG 2024), ArXiv preprint: arXiv:2403.10958
We
extend the persistence algorithm, viewed as an algorithm computing the
homology of a complex of free persistence or graded modules, to
complexes of modules that are not free. We replace persistence modules
by their presentations and develop an efficient algorithm to compute
the homology of a complex of presentations. To deal with inputs that
are not given in terms of presentations, we give an efficient algorithm
to compute a presentation of a morphism of persistence modules. This
allows us to compute persistent (co)homology of instances giving rise
to complexes of non-free modules. Our methods lead to a new efficient
algorithm for computing the persistent homology of simplicial towers
and they enable efficient algorithms to compute the persistent homology
of cosheaves over simplicial towers and cohomology of persistent
sheaves on simplicial complexes. We also show that we can compute the
cohomology of persistent sheaves over arbitrary finite posets by
reducing the computation to a computation over simplicial complexes.
|

|
|
Cup product persistence and its efficient computation
T. K. Dey, A. Rathod. Proc. 40th Internat. Sympos. Comput. Geom. (SoCG 2024), Arxiv preprint: arXiv:2212.01633.
It
is well-known that the cohomology ring has a richer structure than
homology groups. However, until recently, the use of cohomology in
persistence setting has been limited to speeding up of barcode
computations. Some of the recently introduced invariants, namely,
persistent cup-length, persistent cup modules, and persistent Steenrod
modules to some extent, fill this gap. When added to the standard
persistence barcode, they lead to invariants that are more
discriminative than the standard persistence barcode. In this work, we
devise an O(dn^4) algorithm for computing the persistent k-cup modules
for all $k\in\{2,\dots, d\}$, where $d$ denotes the dimension of the
filtered complex, and $n$ denotes its size. Moreover, we note that
since the persistent cup length can be obtained as a byproduct of our
computations, this leads to a faster algorithm for computing it.
Finally, we introduce a new stabble invariant called partition modules
of cup product that is more discriminative than persistent k-cup module
and devise an O(c(d)n^4) time algorithm for compututing it.
|

|
|
Computing zigzag vineyard efficiently including expansions and contractions
T. K. Dey, T. Hou. Proc. 40th Internat. Sympos. Comput. Geom. (SoCG 2024), Arxiv preprint: arXiv:2307.07462.
Vines
and vineyard connecting a stack of persistence diagrams have been
introduced in the non-zigzag setting by Cohen-Steiner et al. We
consider computing these vines over changing filtrations for zigzag
persistence while incorporating two more operations: expansions and
contractions in addition to the transpositions considered in the
non-zigzag setting. Although expansions and contractions can be
implemented in quadratic time in the non-zigzag case by utilizing the
linear-time transpositions, it is not obvious how they can be carried
out under the zigzag framework with the same complexity. While
transpositions alone can be easily conducted in linear time using the
recent FastZigzag algorithm, expansions and contractions pose
difficulty in breaking the barrier of cubic complexity. Our main result
is that, the half-way constructed up-down filtration in the FastZigzag
algorithm indeed can be used to achieve linear time complexity for
transpositions and quadratic time complexity for expansions and
contractions, matching the time complexity of all corresponding
operations in the non-zigzag case.
|

|
|
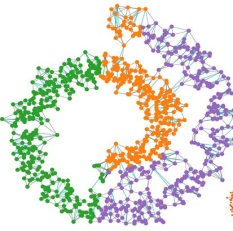
Topological structure of complex predictions
M. Liu, T. K. Dey, D. Gleich. Nature Machine Intelligence, vol. 5, 1382-1389 (2024).
Complex
prediction models such as deep learning are the output from fitting
machine learning, neural networks, or AI models to a set of training
data. These are now standard tools in science. A key challenge with the
current generation of models is that they are highly parameterized,
which makes describing and interpreting the prediction strategies
difficult. We use topological data analysis to transform these complex
prediction models into pictures representing a topological view. The
result is a map of the predictions that enables inspection. The methods
scale up to large datasets across different domains and enable us to
detect labeling errors in training data, understand generalization in
image classification, and inspect predictions of likely pathogenic
mutations in the BRCA1 gene.
|
|
|
Meta-diagrams for 2-parameter persistence
N. Clause, T. K. Dey, F. Memoli, B. Wang. Proc. 39th Internat. Sympos. Comput. Geom. (SoCG 2023), Arxiv preprint: arXiv:2303.08270
We
first introduce the notion of meta-rank for a 2-parameter persistence
module, an invariant that captures the information behind images of
morphisms between 1D slices of the module. We then define the
meta-diagram of a 2-parameter persistence module to be the M\"{o}bius
inversion of the meta-rank, resulting in a function that takes values
from signed 1-parameter persistence modules. We show that the meta-rank
and meta-diagram contain information equivalent to the rank invariant
and the signed barcode. This equivalence leads to computational
benefits, as we introduce an algorithm for computing the meta-rank and
meta-diagram of a 2-parameter module $M$ indexed by a bifiltration of
$n$ simplices in $O(n^3)$ time. This implies an improvement upon the
existing algorithm for computing the signed barcode, which has $O(n^4)$
runtime. This also allows us to improve the existing upper bound on the
number of rectangles in the rank decomposition of $M$ from $O(n^4)$ to
$O(n^3)$. In addition, we define notions of erosion distance between
meta-ranks and between meta-diagrams, and show that under these
distances, meta-ranks and meta-diagrams are stable with respect to the
interleaving distance. Lastly, the meta-diagram can be visualized in an
intuitive fashion as a persistence diagram of diagrams, which
generalizes the well-understood persistence diagram in the 1-parameter
setting.
|

|
|
GRIL: A $2$-parameter persistence based vectorization for machine learning
C. Xin, S. Mukherjee, S.N. Samaga, T. K. Dey Proc. of TAGML 2023, ArXiv preprint: arXiv:2304.04970(2023)
1-parameter
persistence, a cornerstone in Topological Data Analysis (TDA),
studies the evolution of topological features such as connected
components and cycles hidden in data. It has been applied to enhance
the representation power of deep learning models, such as Graph Neural
Networks (GNNs). To enrich the representations of topological
features, here we propose to study 2-parameter persistence
modules induced by bi-filtration functions. In order to incorporate
these representations into machine learning models, we introduce a
novel vector representation called Generalized Rank Invariant Landscape
(GRIL) for 2-parameter persistence modules. We show that this
vector representation is 1-Lipschitz stable and differentiable with
respect to underlying filtration functions and can be easily integrated
into machine learning models to augment encoding topological features.
We present an algorithm to compute the vector representation
efficiently. We also test our methods on synthetic and benchmark graph
datasets, and compare the results with previous vector representations
of 1-parameter and 2-parameter persistence modules. Further, we augment
GNNs with GRIL features and observe an increase in performance
indicating that GRIL can capture additional features enriching GNNs We make the
complete code for the proposed method available
{https://github.com/soham0209/mpml-graph}
Github for software
|

|
|
Computing connection matrices via persistence-like reductions
T. K. Dey, M. Lipinski, M. Mrozek, R. Slechta, SIAM J. Applied Dynamical Systems, Vol. 23, Issue 1, pages 81-97, ArXiv preprint: arXiv:2303.02549(2023)
Connection
matrices are a generalization of Morse boundary operators from the
classical Morse theory for gradient vector fields. Developing an
efficient computational framework for connection matrices is
particularly important in the context of a rapidly growing data science
that requires new mathematical tools for discrete data. Toward this goal, the classical theory for
connection matrices has been adapted to combinatorial frameworks that
facilitate computation. We develop an efficient persistence-like
algorithm to compute a connection matrix from a given combinatorial
(multi) vector field on a simplicial complex. This algorithm requires a
single-pass, improving upon a known algorithm that runs an implicit
recursion executing two-passes at each level. Overall, the new
algorithm is more simple, direct, and efficient than the
state-of-the-art. Because of the algorithm's similarity to the
persistence algorithm, one may take advantage of various software optimizations from topological data analysis.
|

|
|
Revisiting graph persistence for updates and efficiency
T. K. Dey, T. Hou, S. Parsa. Proc. 18th Algorithms and Data Structures Symposium (WADS 2023)
ArXiv preprint: arXiv:2302.12796(2023)
It
is well known that ordinary persistence on graphs can be computed more
efficiently than the general persistence. Recently, it has been
shown that zigzag persistence on graphs also exhibits similar behavior.
Motivated by these results, we revisit graph persistence and propose
efficient algorithms especially for local updates on filtrations,
similar to what is done in ordinary persistence for computing the
vineyard. We show that, for a filtration of length $m$, (i) switches
(transpositions) in ordinary graph persistence can be done in $O(log
m)$ time; (ii) zigzag persistence on graphs can be computed in $O(m log
m)$ time, which improves a recent $O(m log^4n)$ time algorithm assuming
$n$, the size of the union of all graphs in the filtration, satisfies
$n\in\Omega({m^\varepsilon})$ for any fixed $0<\varepsilon<1$;
(iii) open-closed, closed-open, and closed-closed bars in dimension $0$
for graph zigzag persistence can be updated in $O(log m)$ time, whereas
the open-open bars in dimension $0$ and closed-closed bars in dimension
$1$ can be done in $O(\sqrt{m} log m)$ time.
|

|
|
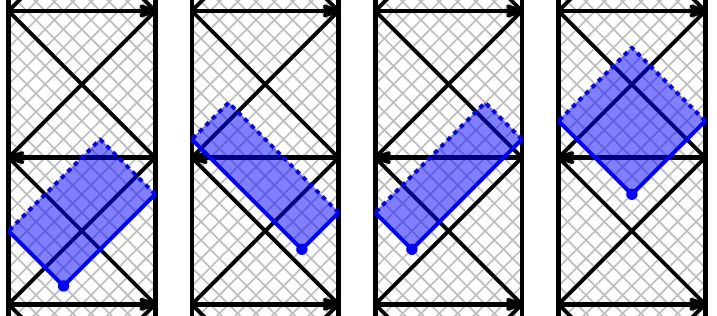
Fast computation of zigzag persistence
T. K. Dey, T. Hou. Proc. 30th European Symposium on Algorithms (ESA 2022), Vol. 244 of LIPIcs, pages 43:1--43:15. ArXiv preprint: arXiv:2204.11080(2022)
[Slides]
Zigzag
persistence is a powerful extension of the standard persistence which
allows deletions of simplices besides insertions. However, computing
zigzag persistence usually takes considerably more time than the
standard persistence. We propose an algorithm called FastZigzag which
narrows this efficiency gap. Our main result is that an input
simplex-wise zigzag filtration can be converted to a cell-wise
non-zigzag filtration of a Δ-complex
with the same length, where the cells are copies of the input
simplices. This conversion step in FastZigzag incurs very little cost.
Furthermore, the barcode of the original filtration can be easily read
from the barcode of the new cell-wise filtration because the conversion
embodies a series of diamond switches known in topological data
analysis. This seemingly simple observation opens up the vast
possibilities for improving the computation of zigzag persistence
because any efficient algorithm/software for standard persistence can
now be applied to computing zigzag persistence. Our experiment shows
that this indeed achieves substantial performance gain over the
existing state-of-the-art softwares.
[Software Download] [AATRN Talk]
This paper originated from: On association between absolute and relative zigzag persistence, ArXiv preprint: arXiv:2110.06315 (2021)
|

|
|
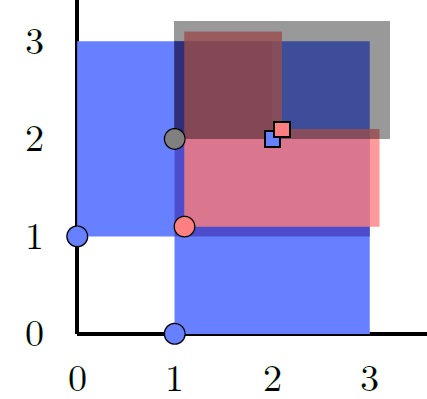
Computing generalized rank invariant for 2-parameter persistence modules via zigzag persistence and its applications
T. K. Dey, W. Kim, and F. Memoli. Proc. 38th Internat. Sympos. Comput. Geom. (SoCG 2022), Vol. 224 of LIPIcs, pages 34:1--34:17, ArXiv preprint: arXiv:2111.15058(2021)
Talk Slides
The
notion of generalized rank invariant in the context of multiparameter
persistence has become an important ingredient for defining interesting
homological structures such as generalized persistence diagrams.
Naturally, computing these rank invariants efficiently is a prelude to
computing any of these derived structures efficiently. We show that the
generalized rank over a finite interval $I$ of a $Z^2$-indexed
persistence module $M$ is equal to the generalized rank of the zigzag
module that is induced on a certain path in $I$ tracing mostly its
boundary. Hence, we can compute the generalized rank over $I$ by
computing the barcode of the zigzag module obtained by restricting the
bifiltration inducing $M$ to that path. If $I$ has $t$ points, this
computation takes $O(t^\omega)$ time where $\omega\in[2,2.373)$ is the
exponent of matrix multiplication. Among others, we apply this result
to obtain an improved algorithm for the following problem. Given a
bifiltration inducing a module $M$, determine whether $M$ is interval
decomposable and, if so, compute all intervals supporting its summands.
Our algorithm runs in time $O(t^{2\omega})$ vastly
improving upon existing algorithms for this problem.
|

|
|
Tracking dynamical features via continuation and persistence
T. K. Dey, M. Lipinsky, M. Mrozek, and R. Slechta. Proc.
38th Internat. Sympos. Comput. Geom. (SoCG 2022), Vol. 224 LIPIcs,
pages 35:1--35:17, ArXiv preprint: https://arxiv.org/abs/2203.05727
Multivector
fields and combinatorial dynamical systems have recently become a
subject of interest due to their potential for use in computational
methods. In this paper, we develop a method to track an isolated
invariant set---a salient feature of a combinatorial dynamical
system---across a sequence of multivector fields. This goal is attained
by placing the classical notion of the ``continuation'' of an isolated
invariant set in the combinatorial setting. In particular, we give a
``Tracking Protocol'' that, when given a seed isolated invariant set,
finds a canonical continuation of the seed across a sequence of
multivector fields. In cases where it is not possible to continue, we
show how to use zigzag persistence to track homological features
associated with the isolated invariant sets. This construction permits
viewing continuation as a special case of persistence.
|

|
|
Updating barcodes and representatives for zigzag persistence
T. K. Dey, and T. Hou, ArXiv preprint: arXiv:2112.02352(2021)
Computing
persistence over changing filtrations give rise to a stack of 2D
persistence diagrams where the birth-death points are connected by the
so-called `vines'. We consider computing these vines over changing
filtrations for zigzag persistence. We observe that eight atomic
operations are sufficient for changing one zigzag filtration to another
and provide update algorithms for each of them. Six of these operations
that have some analogues to one or multiple transpositions in the
non-zigzag case can be executed as efficiently as their non-zigzag
counterparts. This approach takes advantage of a recently discovered
algorithm for computing zigzag barcodes by converting a zigzag
filtration to a non-zigzag one and then connecting barcodes of the two
with a bijection. The remaining two atomic operations do not have a
strict analogue in the non-zigzag case. For them, we propose algorithms
based on explicit maintenance of representatives (homology cycles)
which can be useful in their own rights for applications requiring
explicit updates of representatives.
|

|
|
On association between absolute and relative zigzag persistence
T. K. Dey, and T. Hou, ArXiv preprint: arXiv:2110.06315 (2021)
Duality
results connecting persistence modules for absolute and relative
homology provides a fundamental understanding into persistence theory.
In this paper, we study similar associations in the context of zigzag
persistence. Our main finding is a weak duality for the so-called
non-repetitive zigzag filtrations in which a simplex is never added
again after being deleted. The technique used to prove the duality for
non-zigzag persistence does not extend straightforwardly to our case.
Accordingly, taking a different route, we prove the weak duality by
converting a non-repetitive filtration to an up-down filtration by a
sequence of diamond switches. We then show an application of the weak
duality result which gives a near-linear algorithm for computing the pp-th and a subset of the (p−1)(p-1)-th persistence for a non-repetitive zigzag filtration of a simplicial pp-manifold.
Utilizing the fact that a non-repetitive filtration admits an up-down
filtration as its canonical form, we further reduce the problem of
computing zigzag persistence for non-repetitive filtrations to the
problem of computing standard persistence for which several efficient
implementations exist. Our experiment shows that this achieves
substantial performance gain. Our study also identifies repetitive
filtrations as instances that fundamentally distinguish zigzag
persistence from the standard persistence.
|

|
|
Persistence of Conley-Morse graphs in combinatorial dynamical systems
T. K. Dey, M. Mrozek, and R. Slechta, SIAM J. Applied Dynamical Systems, Vol. 21, Iss. 2, pages 817--839, 2022. Arxiv preprint: https://arxiv.org/abs/2107.02115(2021)
Multivector
fields provide an avenue for studying continuous dynamical systems in a
combinatorial framework. There are currently two approaches in the
literature which use persistent homology to capture changes in
combinatorial dynamical systems. The first captures changes in the
Conley index, while the second captures changes in the Morse
decomposition. However, such approaches have limitations. The former
approach only describes how the Conley index changes across a selected
isolated invariant set though the dynamics can be much more complicated
than the behavior of a single isolated invariant set. Likewise,
considering a Morse decomposition omits much information about the
individual Morse sets. In this paper, we propose a method to summarize
changes in combinatorial dynamical systems by capturing changes in the
so-called Conley-Morse graphs. A Conley-Morse graph contains
information about both the structure of a selected Morse decomposition
and about the Conley index at each Morse set in the decomposition.
Hence, our method summarizes the changing structure of a sequence of
dynamical systems at a finer granularity than previous approaches.
|

|
|
Topological filtering for 3D microstructure segmentation
A. V. Patel, T. Hou, J. D. B. Rodriguez, T. K. Dey, and D. P. Birnie III, Computational Materials Science, 202:110920, 2022.
Tomography
is a widely used tool for analyzing microstructures in three dimensions
(3D). The analysis, however, faces difficulty because the constituent
materials produce similar grey-scale values. Sometimes, this prompts
the image segmentation process to assign a pixel/voxel to the wrong
phase (active material or pore). Consequently, errors are introduced in
the microstructure characteristics calculation. In this work, we
develop a filtering algorithm called PerSplat based on topological
persistence (a technique used in topological data analysis) to improve
segmentation quality. One problem faced when evaluating filtering
algorithms is that real image data in general are not equipped with the
`ground truth' for the microstructure characteristics. For this study,
we construct synthetic images for which the ground-truth values are
known. On the synthetic images, we compare the pore tortuosity and
Minkowski functionals (volume and surface area) computed with our
PerSplat filter and other methods such as total variation (TV) and
non-local means (NL-means). Moreover, on a real 3D image, we visually
compare the segmentation results provided by our filter against TV and
NL-means. The experimental results indicate that PerSplat provides a
significant improvement in segmentation quality.
|

|
|
Appproximating 1-Wasserstein distance between persistence diagrams by graph sparsification
T.
K. Dey, S. Zhang, SIAM Sympos. Algorithm Engg. Experiments (ALENEX22), 2022.
Persistence
diagrams (PDs) play a central role in topological data analysis. This
analysis requires computing distances among such diagrams such as the
1-Wasserstein distance. Accurate computation of these PD distances for
large data sets that render large diagrams may not scale appropriately
with the existing methods. The main source of difficulty ensues from
the size of the bipartite graph on which a matching needs to be
computed for determining these PD distances. We address this problem by
making several algorithmic and computational observations in order to
obtain an approximation. First, taking advantage of the proximity of PD
points, we condense them thereby decreasing the number of nodes in the
graph for computation. The increase in point multiplicities is
addressed by reducing the matching problem to a min-cost flow problem
on a transshipment network. Second, we use Well Separated Pair
Decomposition to sparsify the graph to a size that is linear in the
number of points. Both node and arc sparsifications contribute to the
approximation factor where we leverage a lower bound given by the
Relaxed Word Mover's distance. Third, we eliminate bottlenecks during
the sparsification procedure by introducing parallelism. Fourth, we
develop an open source software called PDoptFlow based on our
algorithm, exploiting parallelism by GPU and multicore. We perform
extensive experiments and show that the actual empirical error is very
low. We also show that we can achieve high performance at low
guaranteed relative errors, improving upon the state of the arts.
|

|
|
Computing optimal persistent cycles for levelset zigzag on manifold-like complexes
T.
K. Dey, T. Hou, arXiv: https://arxiv.org/abs/2105.00518 May 2021.
In
standard persistent homology, a persistent cycle born and dying with a
persistence interval (bar) associates the bar with a concrete
topological representative, which provides means to effectively
navigate back from the barcode to the topological space. Among the
possibly many, optimal persistent cycles bring forth further
information due to having guaranteed quality. However, topological
features usually go through variations in the lifecycle of a bar which
a single persistent cycle may not capture. Hence, for persistent
homology induced from PL functions, we propose levelset persistent
cycles consisting of a sequence of cycles that depict the evolution of
homological features from birth to death. Our definition is based on
levelset zigzag persistence which involves four types of persistence
intervals as opposed to the two types in standard persistence. For each
of the four types, we present a polynomial-time algorithm computing an
optimal sequence of levelset persistent pp-cycles for the so-called weak (p+1)(p+1)-pseudomanifolds.
Given that optimal cycle problems for homology are NP-hard in general,
our results are useful in practice because weak pseudomanifolds do
appear in applications. Our algorithms draw upon an idea of relating
optimal cycles to min-cuts in a graph that we exploited earlier for
standard persistent cycles. Note that levelset zigzag poses non-trivial
challenges for the approach because a sequence of optimal cycles
instead of a single one needs to be computed in this case.
|

|
|
Computing zigzag persistence on graphs in near-linear time
T.
K. Dey, T. Hou, March 2021, Proc. 37th Internat. Sympos. Comput. Geom. (2021), Vol. 189 of LIPIcs, pages 30:1--30:15 (SoCG 2021).
Graphs model real-world circumstances in many
applications where they may constantly change to capture the dynamic
behavior of the phenomena. Topological persistence which provides a set
of birth and death pairs for the topological features is one instrument
for analyzing such changing graph data. However, standard persistent
homology defined over a growing space cannot always capture such a
dynamic process unless shrinking with deletions is also allowed. Hence,
zigzag persistence which incorporates both insertions and deletions of
simplices is more appropriate in such a setting. Unlike standard
persistence which admits nearly linear-time algorithms for graphs, such
results for the zigzag version improving the general $O(m^w)$ time
complexity are not known, where $w< 2.37286$ is the matrix
multiplication exponent. In this paper, we propose algorithms for
zigzag persistence on graphs which run in near-linear time.
Specifically, given a filtration with $m$ additions and deletions on a
graph with $n$ vertices and edges, the algorithm for $0$-dimension runs
in $O(m\log^2 n+m\log m)$ time and the algorithm for 1-dimension runs
in $O(m\log^4 n)$ time.
|

|
|
Persistence of the Conley Index in Combinatorial Dynamical Systems
T.
K. Dey, M. Mrozek, and R. Slechta, February 2020, Proc. Internat. Sympos. Comput. Geom. (2020) (SoCG 2020).
A combinatorial framework for dynamical systems provides an avenue for connecting classical
dynamics with algorithmic methods. Discrete Morse vector fields by
Forman and its recent adaptation to multivector fields by Mrozek have
laid the foundation for this combinatorial framework. In this work, we
make a further connection to computational topology by putting the well
known Conley index of (multi)vector fields into the persistence
framework. Conley indices are homological features of the so called
invariant sets in a dynamical system. We show how one can compute the
persistence of these indices over a sequence of multivector fields
sampled from an underlying dynamical system. This also enables us to
`track' features in a dynamical system in a principled way.
| 
|
|
An efficient algorithm for 1-dimensional (persistent) path homology
T.
K. Dey, T. Li, and Y. Wang, January 2020, arxiv:https://arxiv.org/abs/2001.09549, Proc. Internat. Sympos. Comput. Geom. (2020) (SoCG 2020).
This paper focuses on developing an efficient algorithm for analyzing a
directed network (graph) from a topological viewpoint. A prevalent technique
for such topological analysis involves computation of homology groups and their
persistence. These concepts are well suited for spaces that are not directed.
As a result, one needs a concept of homology that accommodates orientations in
input space. Path-homology developed for directed graphs by Grigor'yan, Lin,
Muranov and Yau has been effectively adapted for this purpose recently by
Chowdhury and Mémoli. They also give an algorithm to compute this
path-homology. Our main contribution in this paper is an algorithm that
computes this path-homology and its persistence more efficiently for the
11-dimensional (H_1H1) case. In developing such an algorithm, we discover
various structures and their efficient computations that aid computing the
1-dimensional path-homnology. We implement our algorithm and present some
preliminary experimental results.
| 
|
|
Road Network reconstruction from Satellite Images with Machine Learning Supported by Topological Methods
T.
K. Dey, J. Wang, and Y. Wang, September 2019, arxiv:https://arxiv.org/pdf/1909.06728.pdf A shoter version to appear in SIGSPATIAL 2019.
Automatic
Extraction of road network from satellite images is a goal that can
benefit and even enable new technologies. Methods that combine machine
learning (ML) and computer vision have been proposed in recent years
which make the task semi-automatic by requiring the user to provide
curated training samples. The process can be fully automatized if
training samples can be produced algorithmically. Of course, this
requires a robust algorithm that can reconstruct the road networks from
satellite images reliably so that the output can be fed as training
samples. In this work, we develop such a technique by infusing a
persistence-guided discrete Morse based graph reconstruction algorithm
into ML framework.
We
elucidate our contributions in two phases. First, in a semi-automatic
framework, we combine a discrete-Morse based graph reconstruction
algorithm with an existing CNN framework to segment input satellite
images. We show that this leads to reconstructions with better
connectivity and less noise. Next, in a fully automatic framework, we
leverage the power of the discrete-Morse based graph reconstruction
algorithm to train a CNN from a collection of images without labelled
data and use the same algorithm to produce the final output from the
segmented images created by the trained CNN. We apply the
discrete-Morse based graph reconstruction algorithm iteratively to
improve the accuracy of the CNN. We show promising experimental results
of this new framework on datasets from SpaceNet Challenge.
| 
|
|
Generalized Persistence Algorithm for Decomposing Multi-parameter Persistence Modules
T.
K. Dey and Cheng Xin, J. Applied and Computational Topology (JACT), 2022. ArXiv version https://arxiv.org/abs/1904.03766.
Link to Journal version
The
classical persistence algorithm computes the unique decomposition of a
persistence module implicitly given by an input simplicial filtration.
Based on matrix reduction, this algorithm is a cornerstone of the
emergent area of topological data analysis. Its input is a simplicial
filtration defined over the integers $\mathbb{Z}$ giving rise to a
$1$-parameter persistence module. It has been recognized that
multiparameter version of persistence modules given by simplicial
filtrations over $d$-dimensional integer grids $\mathbb{Z}^d$ is
equally or perhaps more important in data science applications.
However, in the multiparameter setting, one of the main challenges is
that topological summaries based on algebraic structure such as
decompositions and bottleneck distances cannot be as efficiently
computed as in the $1$-parameter case because there is no known
extension of the persistence algorithm to multiparameter persistence
modules. We present an efficient algorithm to compute the unique
decomposition of a finitely presented persistence module $M$ defined
over the multiparameter $\mathbb{Z}^d$. The algorithm first assumes
that the module is presented with a set of $N$ generators and relations
that are \emph{distinctly graded}. Based on a generalized matrix
reduction technique it runs in $O(N^{2\omega+1})$ time where
$\omega<2.373$ is the exponent of matrix multiplication. This is
much better than the well known algorithm called Meataxe which runs in
$\tilde{O}(N^{6(d+1)})$ time on such an input. In practice, persistence
modules are usually induced by simplicial filtrations. With such an
input consisting of $n$ simplices, our algorithm runs in
$O(n^{(d-1)(2\omega + 1)})$ time for $d\geq 2$. For the special case of
zero dimensional homology, it runs in time $O(n^{2\omega +1})$.
|

|
|
Computing Minimal Persistent Cycles: Polynomial and Hard Cases
T.
K. Dey, T. Hou, and S. Mandal. Proceedings ACM-SIAM Sympos. Discrete Algorithms (SODA 20).
July 2019, arxiv: https://arxiv.org/abs/1907.04889
Persistent cycles, especially the minimal ones, are useful geometric features
functioning as augmentations for the intervals in the purely topological
persistence diagrams (also termed as barcodes). In our earlier work, we showed
that computing minimal 1-dimensional persistent cycles (persistent 1-cycles)
for finite intervals is NP-hard while the same for infinite intervals is
polynomially tractable. In this paper, we address this problem for general
dimensions with Z2 coefficients. In addition to proving that it is NP-hard
to compute minimal persistent d-cycles (d>1) for both types of intervals given
arbitrary simplicial complexes, we identify two interesting cases which are
polynomially tractable. These two cases assume the complex to be a certain
generalization of manifolds which we term as weak pseudomanifolds. For finite
intervals from the d-th persistence diagram of a weak (d+1)-pseudomanifold, we
utilize the fact that persistent cycles of such intervals are null-homologous
and reduce the problem to a minimal cut problem. Since the same problem for
infinite intervals is NP-hard, we further assume the weak (d+1)-pseudomanifold
to be embedded in R^{d+1}Rd+1 so that the complex has a natural dual
graph structure and the problem reduces to a minimal cut problem. Experiments
with both algorithms on scientific data indicate that the minimal persistent
cycles capture various significant features of the data.
|

|
|
Petsistent 1-Cycles: Definition, Computation, and Its Application
T.
K. Dey , T. Hou, and S. Mandal . Proceedings Computational Topology in Image Context (CTIC 2019), LNCS, Vol. 11382, pages 123--136.
arxiv version: https://arxiv.org/abs/1810.04807
See this web-page for software etc.: http://web.cse.ohio-state.edu/~dey.8/PersLoop/
Persistence
diagrams, which summarize the birth and death of homological features
extracted from data, are employed as stable signatures for applications
in image analysis and other areas. Besides simply considering the
multiset of intervals included in a persistence diagram, some
applications need to find representative cycles for the intervals. In
this paper, we address the problem of computing these representative
cycles, termed as persistent $1$-cycles.
The definition of persistent cycles is based on the interval module
decomposition of persistence modules, which reveals the structure of
persistent homology. After showing that the computation of the optimal
persistent $1$-cycles is NP-hard, we propose an alternative set
of meaningful persistent
$1$-cycles that can be computed with an efficient polynomial time
algorithm. We also inspect the stability issues of the optimal
persistent $1$-cycles and the persistent $1$-cycles computed by our
algorithm with the observation that the perturbations of both cannot be
properly bounded. We design a software which applies our algorithm to
various datasets. Experiments on 3D point clouds, mineral structures,
and images show the effectiveness of our algorithm in practice.
| 
|
|
Filtration simplification for persistent homology via edge contraction
T.
K. Dey , R. Slechta. Internat. Conf. Discrete Geoem. for Comput. Imagery (DGCI 2019), pages 89--100 .
arxiv version: https://arxiv.org/abs/1810.04388
See this web-page for software: https://github.com/rslechta/pers-contract/
Persistent
homology is a popular data analysis technique that is used to capture
the changing topology of a filtration associated with some simplicial
complex $K$. These topological changes are summarized in persistence
diagrams. We propose two contraction operators which when applied to
$K$ and its associated filtration, bound the perturbation in the
persistence diagrams. The first assumes that the underlying space of
$K$ is a $2$-manifold and ensures that simplices are paired with the
same simplices in the contracted complex as they are in the original.
The second is for arbitrary $d$-complexes, and bounds the bottleneck
distance between the initial and contracted $p$-dimensional persistence
diagrams. This is accomplished by defining interleaving maps between
persistence modules which arise from chain maps defined over the
filtrations. In addition, we show how the second operator can
efficiently compose across multiple contractions. We conclude with
experiments demonstrating the second operator's utility on manifolds.
| 
|
|
Computing height persistence and homology generators in R^3 efficiently
T.
K. Dey , Proc. 30th ACM-SIAM Sympos. Discrete Algorithms, 2019 (SODA 19), pages 2649--2662.
arxiv version: https://arxiv.org/abs/1807.03655
Talk Slides
Recently
it has been shown that computing the dimension of the first
homology group $H_1(K)$ of a simplicial $2$-complex $K$ embedded
linearly in $R^4$ is as hard as computing the rank of a sparse
$0-1$ matrix. This puts a major roadblock to computing
persistence and a homology basis (generators) for complexes
embedded in $R^4$ and beyond in less than quadratic or even
near-quadratic time. But, what about dimension three? It is known
that persistence for piecewise linear functions on a complex $K$ with
$n$ simplices can be computed in $O(n\log n)$ time and a set of
generators of total size $k$ can be computed in $O(n+k)$ time when $K$
is a graph or a surface linearly embedded in $R^3$. But, the
question for general simplicial complexes $K$ linearly embedded
in $R^3$ is not completely settled. No algorithm with a complexity
better than that of the matrix multiplication is known for
this important case. We show that the persistence for {\em height
functions} on such complexes, hence called {\em height
persistence}, can be computed in $O(n\log n)$ time. This
allows us to compute a basis (generators) of $H_i(K)$, $i=1,2$, in
$O(n\log n+k)$ time where $k$ is the size of the output. This improves
significantly the current best bound of $O(n^{\omega})$, $\omega$ being
the matrix multiplication exponent. We achieve these improved
bounds by leveraging recent results on zigzag persistence in
computational topology, new observations about Reeb graphs, and some
efficient geometric data structures.
|

|
|
Edge contraction in persistence-generated discrete Morse vector fields
T.
K. Dey and R. Slechta. Proc. SMI 2018, Computers & Graphics, .Vol. 74, 33-43.
Journal version: https://doi.org/10.1016/j.cag.2018.05.002
Recently,
discrete Morse vector fields have been shown to be useful in various
applications. Analogous to the simplification of large meshes using
edge contractions, one may want to simplify the cell complex $K$ on
which a discrete Morse vector field $V(K)$ is defined. To this end, we
define a gradient aware edge contraction operator for triangulated
$2$-manifolds with the following guarantee. If $V(K)$ was generated by
a specific persistence-based method, then the vector field that results
from our contraction operator is exactly the same as the vector field
produced by applying the same persistence-based method to the
contracted complex. An implication of this result is that local
operations on $V(K)$ are sufficient to produce the persistence-based
vector field on the contracted complex. Furthermore, our experiments
show that the structure of the vector field is largely preserved by our
operator. For example, $1$-unstable manifolds remain largely unaffected
by the contraction. This suggests that for some applications of
discrete Morse theory, it is sufficient to use a contracted complex.
Also, see our recent work on Discrete Morse based reconstruction here and here
| 
|
|
Persistent homology of Morse decompositions in combinatorial dynamics
T.
K. Dey, M. Juda, T. Kapela, J. Kubica, M. Lipinski, M. Mrozek. https://arxiv.org/abs/1801.06590. 2018. SIAM J. on Applied Dynamical System, Vol. 18, Issue 1, 510--530, 2019.
We investigate combinatorial dynamical systems on simplicial complexes considered as finite topological spaces.
Such systems arise in a natural way from sampling dynamics and may be
used to reconstruct some features of the dynamics directly from
the sample. We study the homological persistence of Morse decompositions
of such systems, an important descriptor of the dynamics, as a
tool for validating the reconstruction. Our framework can be viewed as
a step toward extending the classical persistence theory to ``vector
cloud" data. We present experimental results on two numerical
examples.
| 
|
|
Here is the n-D version of the SoCG paper.
Computing Bottelneck Distance for Multi-parameter Interval Decomposable Persistence Modules
Preprint, September, 2019.
Computing Bottleneck Distance for 2-D Interval Decomposable Modules
T.
K. Dey, C. Xin. Proc. 34th Internat. Sympos. Comput. Geoem., 32:1--32:15 (SoCG 2018).
Computation
of the interleaving distance between persistence modules is a central
task in topological data analysis. For $1$-D persistence modules,
thanks to the isometry theorem, this can be done by computing the
bottleneck distance with known efficient algorithms. The question is
open for most $n$-D persistence modules, $n>1$, because of the well
recognized complications of the indecomposables. Here, we consider a
reasonably complicated class called {\em $2$-D interval decomposable}
modules whose indecomposables may have a description of non-constant
complexity. We present a polynomial time algorithm to compute the
bottleneck distance for these modules from indecomposables, which
bounds the interleaving distance from above, and give another algorithm
to compute a new distance called {\em dimension distance} that bounds
it from below.
|

|
|
Graph Reconstruction by Discrete Morse Theory
T.
K. Dey, J. Wang and Y. Wang. Proc. Internat. Sympos. Comput. Geom., 31:1--31:15 (SoCG 2018).
Recovering hidden graph-like structures from potentially noisy data is a
fundamental task in modern data analysis. Recently, a persistence-guided
discrete Morse-based framework to extract a geometric graph from
low-dimensional data has become popular. However, to date, there is very
limited theoretical understanding of this framework in terms of graph
reconstruction. This paper makes a first step towards closing this gap.
Specifically, first, leveraging existing theoretical understanding of
persistence-guided discrete Morse cancellation, we provide a simplified version
of the existing discrete Morse-based graph reconstruction algorithm. We then
introduce a simple and natural noise model and show that the aforementioned
framework can correctly reconstruct a graph under this noise model, in the
sense that it has the same loop structure as the hidden ground-truth graph, and
is also geometrically close. We also provide some experimental results for our
simplified graph-reconstruction algorithm.
Also see this paper in SIGSPATIAL (2017).
Improved Road Network Reconstruction Using Discrete Morse Theory. T. K. Dey, J. Wang, and Y. Wang. Proc. SIGSPATIAL 2017.
| 
|
|
Application of Topological Data Analysis in Machine Learning for Image and Protein Classification
|
Protein Classification with Improved Topological Data Analysis
T. K. Dey and S. Mandal. Proc. Workshop on Algorithms in Bioinformatics (WABI 2018), 6:1--6:13. DOI 10.4230/LIPIcs.WABI.2018.6
Web-page: http://web.cse.ohio-state.edu/~dey.8/proteinTDA/
Automated annotation and analysis of protein molecules have long been a topic of interest due to
immediate applications in medicine and drug design. In this work, we propose a topology based,
fast, scalable, and parameter-free technique to generate protein signatures.
We build an initial simplicial complex using information about the protein’s constituent atoms,
including radius and existing chemical bonds, to model the hierarchical structure of the molecule.
Simplicial collapse is used to construct a filtration which we use to compute persistent homology.
This information constitutes our signature for the protein. In addition, we demonstrate that this
technique scales well to large proteins. Our method shows sizable time and memory improvements
compared to other topology based approaches. We use the signature to train a protein domain
classifier. Finally, we compare this classifier against models built from state-of-the-art structure-
based protein signatures on standard datasets to achieve a substantial improvement in accuracy.
Improved Image Classification using Topological Persistence
T.
K. Dey, S. Mandal, W. Varcho. Proc. Vision Modeling and Visualization., (VMV 2017). http://dx.doi.org/10.2312/vmv.20171272
Web-page: http://web.cse.ohio-state.edu/~dey.8/imagePers/
Image classification has been a topic of interest for many years. With
the advent of Deep Learning, impressive progress has been made on the
task, resulting in quite accurate classification. Our work focuses on
improving modern image classification techniques by considering
topological features as well. We show that incorporating this
information allows our models to improve the accuracy, precision and
recall on test data, thus providing evidence that topological signatures
can be leveraged for enhancing some of the state-of-the art
applications in computer vision.
| 
|
|
Efficient Algorithms for Computing a Minimal Homology Basis
T.
K. Dey, T. Li, and Y. Wang. Proc. LATIN 2018: Theoretical Informatics, LNCS, Vol. 10807, 376--398 (LATIN 2018).
Efficient
computation of shortest cycles which form a homology basis
under Z2-additions in a given simplicial complex K has been
researched actively in recent years. When the complex K is a weighted
graph with n vertices and m edges, the problem of computing a
shortest (homology) cycle basis is known to be solvable in $O(m^2n/\log
n+ n^2m)$-time. Several works [1,2] have addressed the case when the
complex K is a 2-manifold. The complexity of these algorithms
depends on the rank g of the one-dimensional homology group of K.
This rank g has a lower bound of $\Theta(n)$, where n denotes the
number of simplices in K giving an $O(n^4)$ worst-case time complexity
for the algorithms in [1,2]. This worst-case complexity is improved in
[3] to $O(n^\omega+n^2g^{\omega-1})$ for general simplicial complexes
where $\omega< 2.3728639$ [4] is the matrix multiplication exponent.
Taking $g=\Theta(n)$, this provides an $O(n^{\omega+1})$ worst-case
algorithm. In this paper, we improve this time complexity.
Combining the divide and conquer technique from [5] with the use
of annotations from [3], we present an algorithm that runs in
$O(n^\omega+n^2g)$ time giving the first $O(n^3)$ worst-case algorithm
for general complexes. If instead of minimal basis, we settle for
approximate basis, we can improve the running time even further. We
show that a 2-approximate minimal homology basis can be computed
in $O(n^{\omega}\sqrt{n \log n})$ expected time. We also study more
general measures for defining the minimal basis and identify reasonable
conditions on these measures that allow computing a minimal basis
efficiently.
|
|
|
Temporal Hierarchical Clustering
T.
K. Dey, A. Rossi, and A. Sidiropoulos. Proc. 28th Internat. Symposium on Algorithms and Computation (ISAAC 2017).
https://arxiv.org/abs/1707.09904
We study hierarchical clusterings of metric spaces that change over time.
This is a natural geometric primitive for the analysis of dynamic data sets.
Specifically, we introduce and study the problem of finding a temporally
coherent sequence of hierarchical clusterings from a sequence of unlabeled
point sets. We encode the clustering objective by embedding each point set into
an ultrametric space, which naturally induces a hierarchical clustering of the
set of points. We enforce temporal coherence among the embeddings by finding
correspondences between successive pairs of ultrametric spaces which exhibit
small distortion in the Gromov-Hausdorff sense. We present both upper and lower
bounds on the approximability of the resulting optimization problems.
| 
|
|
Temporal Clustering
T.
K. Dey, A. Rossi, and A. Sidiropoulos. Proc. European Symposium on Algorithms (ESA 2017).
Full Version
https://arxiv.org/abs/1704.05964
We study the problem of clustering sequences of unlabeled point
sets taken from a common metric space. Such scenarios arise naturally
in applications where a system or process is observed in distinct time
intervals, such as biological surveys and contagious disease
surveillance. In this more general setting existing algorithms for
classical (i.e.~static) clustering problems are not applicable anymore.
We propose a set of optimization problems which we collectively refer
to as \emph{temporal clustering}. The quality of a solution to a
temporal clustering instance can be quantified using three parameters:
the number of clusters $k$, the spatial clustering cost $r$, and the
maximum cluster displacement $\delta$ between consecutive time steps.
We consider spatial clustering costs which
generalize the well-studied $k$-center, discrete $k$-median, and
discrete $k$-means objectives of classical clustering problems. We
develop new algorithms that achieve trade-offs between the three
objectives $k$, $r$, and $\delta$. Our upper bounds are complemented by
inapproximability results.
|

|
|
Topological analysis of nerves, Reeb spaces, mappers, and multiscale mappers
T.
K. Dey, F. Memoli, and Y. Wang. Proc. Internat. Sympos. Comput. Geom. (2017) (SoCG 2017).
Full Version
[talk slides]
Data analysis
often concerns not only the space where data come from, but also
various types of maps attached to data. In recent years, several
related structures have been used to study maps on data, including Reeb
spaces, mappers and multiscale mappers. The construction of these
structures also relies on the so-called \emph{nerve} of a cover of the
domain.
In this paper, we aim to analyze the topological information
encoded in these structures in order to provide better understanding of
these structures and facilitate their practical usage.
More specifically, we show that the one-dimensional homology of
the nerve complex $N(\mathcal{U})$ of a path-connected cover
$\mathcal{U}$ of a domain $X$ cannot be richer than that of the domain
$X$ itself. Intuitively, this result means that no new $H_1$-homology
class can be ``created'' under a natural map from $X$ to the nerve
complex $N(\mathcal{U})$. Equipping $X$ with a pseudometric $d$, we
further refine this result and characterize the classes of $H_1(X)$
that may survive in the nerve complex using the notion of \emph{size}
of the covering elements in $\mathcal{U}$. These fundamental results
about nerve complexes then lead to an analysis of the $H_1$-homology of
Reeb spaces, mappers and multiscale mappers.
The analysis of $H_1$-homology groups unfortunately does not
extend to higher dimensions. Nevertheless, by using a map-induced
metric, establishing a Gromov-Hausdorff convergence result between
mappers and the domain, and interleaving relevant modules, we can still
analyze the persistent homology groups of (multiscale) mappers to
establish a connection to Reeb spaces.
|

|
|
Declutter and resample: Towards parameter free denoising
M. Buchet, T.
K. Dey, J. Wang, and Y. Wang. Proc. Internat. Sympos. Comput. Geom. (2017), (SoCG 2017).
Full Version
[talk slides]
In many data analysis applications the following scenario is commonplace: we
are given a point set that is supposed to sample a hidden ground truth
$K$ in a metric space, but it got corrupted with noise so that some of
the data points lie far away from $K$ creating outliers also
termed as {\em ambient noise}. One of the main goals of denoising
algorithms is to eliminate such noise so that the curated data lie
within a bounded Hausdorff distance of $K$. Popular denoising
approaches such as deconvolution and thresholding often require the
user to set several parameters and/or to choose an appropriate noise
model while guaranteeing only asymptotic convergence. Our goal is to
lighten this burden as much as possible while ensuring theoretical
guarantees in all cases.
Specifically, first, we propose a simple denoising algorithm that
requires only a single parameter but provides a theoretical guarantee
on the quality of the output on general input points. We argue that
this single parameter cannot be avoided. We next present a simple
algorithm that avoids even this parameter by paying for it with a
slight strengthening of the sampling condition on the input points
which is not unrealistic. We also provide some preliminary empirical
evidence that our algorithms are effective in practice.
|

|
|
Parameter-free topology inference and sparsification for data on manifolds
T.
K. Dey, Z. Dong, and Y. Wang. (2015), older version at arXiv:1505.06462. Proc. ACM-SIAM Sympos. Discrete Algorithms (SODA 2017).
[talk slides]
In topology inference from data, current approaches face two major problems.
One concerns the selection of a correct parameter to build an appropriate
complex on top of the data points; the other involves with the typical `large'
size of this complex. We address these two issues in the context of inferring
homology from sample points of a smooth manifold of known dimension sitting in
an Euclidean space Rk. We show that, for a sample size of n n
points, we can identify a set of O(n2)O(n^2) points (as opposed to O(n⌈k2⌉)O(n^\ceil{k/2}) Voronoi vertices) approximating a subset of the medial
axis that suffices to compute a distance sandwiched between the well known
local feature size and the local weak feature size (in fact, the approximating
set can be further reduced in size to O(n) O(n)). This distance, called the lean
feature size, helps pruning the input set at least to the level of local
feature size while making the data locally uniform. The local uniformity in
turn helps in building a complex for homology inference on top of the
sparsified data without requiring any user-supplied distance threshold. Unlike
most topology inference results, ours does not require that the input is dense
relative to a {\em global} feature such as {\em reach} or {\em weak feature
size}; instead it can be adaptive with respect to the local feature size. We
present some empirical evidence in support of our theoretical claims.
| 
|
|
SimBa: An efficient tool for approximating Rips-filtration persistence via Simplicial Batch-collapse
T.
K. Dey, D. Shi, and Y. Wang. European Symposium on Algorithms (ESA 2016).
An Extended Version.
[talk slides]
SimBa Software
SimPers Software
In
topological data analysis, a point cloud data P extracted from a metric
space is often analyzed by computing the persistence diagram or
barcodes of a sequence of Rips complexes built on P indexed by a scale
parameter. Unfortunately, even for input of moderate size, the size of
the Rips complex may become prohibitively large as the scale parameter
increases. Starting with the \emph{Sparse Rips filtration} introduced
by Sheehy, some existing methods aim to reduce the size of the complex
so as to improve the time efficiency as well. However, as we
demonstrate, existing approaches still fall short of scaling well,
especially for high dimensional data. In this paper, we investigate the
advantages and limitations of existing approaches. Based on insights
gained from the experiments, we propose an efficient new algorithm,
called SimBa, for
approximating the persistent homology of Rips filtrations with quality
guarantees. Our new algorithm leverages a batch collapse strategy as
well as a new sparse Rips-like filtration. We experiment on a variety
of low and high dimensional data sets. We show that our strategy
presents a significant size reduction, and our algorithm for
approximating Rips filtration persistence is order of magnitude faster
than existing methods in practice.
| 
|
|
Multiscale Mapper: Topological summarization via codomain covers
T.
K. Dey, F. Memoli, and Y. Wang. ACM-SIAM Sympos. Discrete Algorithms (SODA 2016) Older version arXiv: 1504.03763v1
[talk slides]
SODA version
Summarizing topological information from datasets and maps defined on them is a central theme in topological data analysis. Mapper,
a tool for such summarization, takes as input both a possibly high
dimensional dataset and a map defined on the data, and produces a
summary of the data by using a cover of the codomain of the map. This
cover, via a pullback operation to the domain, produces a simplicial
complex connecting the data points. The resulting view of the data
through a cover of the codomain offers flexibility in analyzing the
data. However, it offers only a view at a fixed scale at which the
cover is constructed. Inspired by the concept, we explore a notion of
hierarchical family of coverings which induces a hierarchical family of
simplicial complexes connected by simplicial maps, which we call multiscale mapper.
We study the resulting structure, its associated persistence module,
and its stability under perturbations of the maps and the coverings.
The information encoded in multiscale mapper complements that of
individual mappers at fixed scales. An upshot of this development is a
practical algorithm for computing the persistence diagram of multiscale
mapper when the domain is a simplicial complex and the map is a
real-valued piecewise-linear function.
| 
|
|
Segmenting a surface mesh into pants using Morse theory
M. Hajij, T. K. Dey, and X. Li. Graphical Models, Vol 88 (2016), 12--21.
http://www.sciencedirect.com/science/article/pii/S1524070316300376
A
pair of pants is a genus zero orientable surface with three boundary
components. A pants decomposition of a surface is a finite collection
of unordered pairwise disjoint simple closed curves embedded in the
surface that decompose the surface into pants. In this paper, we
present two Morse theory based algorithms for pants decomposition of a
surface mesh. Both algorithms operate on achoice of an appropriate
Morse function on the surface. The first algorithm uses this Morse
function to identify handles that are glued systematically to obtain a
pants decomposition. The second algorithm uses the Reeb graph of the
Morse function to obtain a pants decomposition. Both algorithms work
for surfaces with or without boundaries. Our perliminary implementation
of the two algorithms shows that both algorithms run in much less time
than an existing state-of-the-art method, and the Reeb graph based
algorithm achieves the best time efficiency. Finally, we demonstrate
the robustness of our algorothms agaisnt noise.
|  |
|
Comparing graphs via persistence distortion
T.
K. Dey, D. Shi and Y. Wang. 31st Annu. Sympos. Comput. Geom. (SoCG 15).
[GraphComp software]
Metric graphs are ubiquitous in
science and engineering. For example, many data are drawn from hidden
spaces that are graph-like, such as the cosmic web. A metric graph
offers one of the simplest yet still meaningful ways to represent the
non-linear structure hidden behind the data. In this paper, we propose
a new distance between two finite metric graphs, called the persistence
distortion-distance, which draws upon a topological idea. This
topological perspective along with the metric space viewpoint provide a
new angle to the graph matching problem. Our persistence-distortion
distance has two properties not shared by previous methods: First, it
is stable against the perturbations of the input graph metrics. Second,
it is a \emph{continuous} distance measure, in the sense that it is
defined on an alignment of the underlying spaces of input graphs,
instead of merely their nodes. This makes our persistence-distortion
distance robust against, for example, different discretizations of the
same underlying graph. Despite considering the input graphs as
continuous spaces, that is, taking all points into account, we show
that we can compute the persistence-distortion distance in polynomial
time. The time complexity for the discrete case where only graph nodes
are considered is much faster. We also provide some preliminary
experimental results to demonstrate the use of the new distance measure.
| 
|
|
Topological analysis of scalar fields with outliers
M. Buchet, F. Chazal, T.
K. Dey, F. Fan, S. Oudot and Y. Wang. 31st Annu. Sympos. Comput. Geom. (SoCG 15).
arXiv:1412.1680.
Given a real-valued function ff defined over a manifold MM embedded in
R^dRd, we are interested in recovering structural information about
f f from the sole information of its values on a finite sample PP. Existing
methods provide approximation to the persistence diagram of ff when the noise
is bounded in both the functional and geometric domains. However, they fail in
the presence of aberrant values, also called outliers, both in theory and
practice.
We propose a new algorithm that deals with outliers. We handle aberrant
functional values with a method inspired from the k-nearest neighbors
regression and the local median filtering, while the geometric outliers are
handled using the distance to a measure. Combined with topological results on
nested filtrations, our algorithm performs robust topological analysis of
scalar fields in a wider range of noise models than handled by current methods.
We provide theoretical guarantees on the quality of our approximation and some
experimental results illustrating its behavior.
|

|
|
Spectral concentration and greedy k-clustering
T. K. Dey, A. Rossi., and A. Sidiropoulos, arXiv:1404.1008v2. Comput. Geom. Theory & Applications (2018), to appear.
A popular graph clustering method is to consider the embedding of an input
graph into R^k induced by the first k eigenvectors of its Laplacian, and to
partition the graph via geometric manipulations on the resulting metric space.
Despite the practical success of this methodology, there is limited
understanding of several heuristics that follow this framework. We provide
theoretical justification for one such natural and computationally efficient
variant.
Our result can be summarized as follows. A partition of a graph is called
strong if each cluster has small external conductance, and large internal
conductance. We present a simple greedy spectral clustering algorithm which
returns a partition that is provably close to a suitably strong partition,
provided that such a partition exists. A recent result shows that strong
partitions exist for graphs with a sufficiently large spectral gap between the
k-th and (k+1)-th eigenvalues. Taking this together with our main theorem gives
a spectral algorithm which finds a partition close to a strong one for graphs
with large enough spectral gap. We also show how this simple greedy algorithm
can be implemented in near-linear time for any fixed k and error guarantee.
Finally, we evaluate our algorithm on some real-world and synthetic inputs.
|

|
|
Dimenison detection with local homology
T. K. Dey, F. Fan, and Y. Wang, Canadian Conf. Comput. Geom. (CCCG 2014), Full version arXiv: 1405.3534
[Talk Slide]
Detecting the dimension of a hidden manifold from a point sample has
become an important problem in the current data-driven era. Indeed,
estimating the shape dimension is often the first step in studying the
processes or phenomena associated to the data. Among the many
dimension detection algorithms proposed in various fields, a few can
provide theoretical guarantee on the correctness of the estimated
dimension. However, the correctness usually requires certain regularity
of the input:
the input points are either uniformly randomly sampled in a statistical
setting, or they form the so-called $(\eps,\delta)$-sample which can be
neither too dense nor too sparse.
Here, we propose a purely topological technique to detect dimensions.
Our algorithm is provably correct and works under a more relaxed
sampling condition: we do not require uniformity, and we also allow
Hausdorff noise. Our approach detects dimension by determining local
homology. The computation of this topological structure is much less
sensitive to the local distribution of points, which leads to the
relaxation of the sampling conditions. Furthermore, by leveraging
various developments in computational topology, we show that this local
homology at a point $z$ can be computed \emph{exactly} for manifolds
using Vietoris-Rips complexes whose vertices are confined within a
local neighborhood of $z$. We implement our algorithm and demonstrate
the accuracy and robustness of our method using both synthetic and real
data sets.
|

|
|
Computing topological persistence for simplicial maps
T. K. Dey, F. Fan, and Y. Wang., (SoCG 2014), Proc. 30th Annu. Sympos. Comput. Geom. (2013).
(our algorithm works for any finite field--see the conclusion of updated Full version)
[SimpPers software] [Talk slide]
Algorithms
for persistent homology and zigzag persistent homology are well-studied
for homology modules where homomorphisms are induced by inclusion maps.
In this paper, we propose a practical algorithm for computing
persistence under Z_2 coefficients for a sequence of general
simplicial maps.
First, we observe that it is not hard to simulate simplicial maps by
inclusion maps but not necessarily in a monotone direction. This,
combined with the known algorithms for zigzag persistence, provides an
algorithm for computing the persistence induced by simplicial maps.
Our main result is that the above simple minded approach can be
improved for a sequence of simplicial maps given in a monotone
direction. The improvement results from the use of the so-called
annotations that we show can determine the persistence of simplicial
maps using a lighter data structure. A consistent annotation through
atomic operations implies the maintenance of a consistent cohomology
basis, hence a homology basis by duality. While the idea of maintaining
a cohomology basis through an inclusion is not new, maintaining them
through a vertex collapse is new, which constitutes an important atomic
operation for simulating simplicial maps. Annotations support the
vertex collapse in addition to the usual inclusion quite naturally.
Finally, we exhibit an application of this new tool in which we
approximate the persistence diagram of a filtration of Rips complexes
where vertex collapses are used to tame the blow-up in size.
|

|
|
Automatic posing of meshed human model using point clouds
T. K. Dey, B. Fu, H. Wang, and L. Wang., (SMI 2014), Computers & Graphics, Vol. 46, pages 14--24.
[Talk slide] [Video link]
We introduce a markerless approach to deform a quality human body
template mesh from its original pose to a different pose specified by a
point cloud. The point cloud may be noisy, incomplete, or even captured
from a different person. In this approach, we first build coarse
correspondences between the template mesh and the point cloud through a
squeezed spectral embedding technique that exploits human body
extremities. Based on these correspondences, we define the goal of
non-rigid registration using an elastic energy functional and apply a
discrete gradient flow to reduce the difference between a coarse control
mesh and the point cloud. The deformed template mesh can then be
obtained from the deformation of the control mesh using mean value
coordinates afterwards. Our experiments show (see the supplementary
video) that the approach is capable of equipping a mesh with the pose of
a scanned point cloud data even if it is incomplete and noisy.
|

|
|
Edge contractions and simplicial homology
T. K. Dey, A. N. Hir ani, B. Krishnamoorthy, and G. Smith. April, 2013. arXiv:1304.0664
We study the effect
of edge contractions on simplicial homology because these
contractions have turned to be useful in various applications
involving topology. It was observed previously that contracting
edges that satisfy the so called link condition preserves
homeomorphism in low dimensional complexes, and homotopy in
general. But, checking the link condition involves computation
in all dimensions, and hence can be costly, especially in high
dimensional complexes. We define a weaker and more local
condition called the p-link condition for each dimension
p, and study its effect on edge contractions. We prove the
following: (i) For homology groups, edges satisfying the p-
and (p-1)-link conditions can be contracted without disturbing
the p-dimensional homology group. (ii) For relative homology groups, the (p-1)-, and the (p-2)-link
conditions suffice to guarantee that the contraction does not
introduce any new class in any of the resulting relative
homology groups, though some of the existing classes can be
destroyed. Unfortunately, the surjection in relative homolgy
groups does not guarantee that no new relative torsion is
created. (iii) For torsions, edges satisfying the p-link condition
alone can be contracted without creating any new relative torsion and
the p-link condition cannot be avoided. The results on
relative homology and relative torsion are motivated by recent
results on computing optimal homologous chains, which state that
such problems can be solved by linear programming if the complex
has no relative torsion. Edge contractions that do not
introduce new relative torsions, can safely be availed in these
contexts.
|

|
|
Graph induced complex on point data (full version)
T. K. Dey, F. Fan, and Y. Wang., (SoCG 2013) Proc. 29th Annu. Sympos. Comput. Geom. (2013), pages 107--116.
[Talk slides] [Web-page] [GICsoftware]
The
efficiency of extracting topological information from point data
depends largely on the complex that is built on top of the data points.
From a computational viewpoint, the most favored complexes for this
purpose have so far been Vietoris-Rips and witness complexes. While the
Vietoris-Rips complex is simple to compute and is a good vehicle for
extracting topology of sampled spaces, its size is huge--particularly
in high dimensions. The witness complex on the other hand enjoys a
smaller size because of a subsampling, but fails to capture the
topology in high dimensions unless imposed with extra structures. We
investigate a complex called the graph induced complex that, to
some extent, enjoys the advantages of both. It works on a subsample but
still retains the power of capturing the topology as the Vietoris-Rips
complex. It only needs a graph connecting the original sample points
from which it builds a complex on the subsample thus taming the size
considerably. We show that, using the graph induced complex one can (i)
infer the one dimensional homology of a manifold from a very lean
subsample, (ii) reconstruct a surface in three dimension from a sparse
subsample without computing Delaunay triangulations, (iii) infer the
persistent homology groups of compact sets from a sufficiently dense
sample. We provide experimental evidences in support of our theory.
|

|
|
The compressed annotation matrix: an efficient data structure for computing persistent cohomology.
J.-D. Boissonnat, T. K. Dey, C. Maria, (ESA 2013), LNCS 8125, 2013.
Persistent homology with coefficients in a field F
coincides with the same for cohomology because of duality. We propose
an implementation of a recently introduced algorithm for persistent
cohomology that attaches annotation vectors with the simplices. We
separate the representation of the simplicial complex from the
representation of the cohomology groups, and introduce a new data
structure for maintaining the annotation matrix, which is more compact
and reduces substancially the amount of matrix operations. In addition,
we propose a heuristic to simplify further the representation of the
cohomology groups and improve both time and space complexities. The
paper provides a theoretical analysis, as well as a detailed
experimental study of our implementation and comparison with
state-of-the-art software for persistent homology and cohomology.
Note: Also see our ``computing topological persistence for simplicial maps" paper which motivated this implementation.
|
|
|
An efficient computation of handle and tunnel loops via Reeb graphs.
T. K. Dey, F. Fan, and Y. Wang. ACM Trans. Graphics (Siggraph 2013), Vol. 32 (4). Supplementary file for proofs.
[Web-page] [Software ReebHanTun] [Talk slides]
A special family of non-trivial loops on a surface called
handle and tunnel loops associates closely to geometric features of
``handles" and ``tunnels" respectively in a 3D model. The
identification of these handle and tunnel loops can benefit a broad
range of applications from topology simplification / repair, and
surface parameterization, to feature and shape recognition. Many of the
existing efficient algorithms for computing non-trivial loops cannot be
used to compute these special type of loops. The two algorithms known
for computing handle and tunnel loops provably have a serious drawback
that they both require a tessellation of the interior and exterior
spaces bounded by the surface. Computing such a tessellation of three
dimensional space around the surface is a non-trivial task and can be
quite expensive. Furthermore, such a tessellation may need to refine
the surface mesh, thus causing the undesirable side-effect of
outputting the loops on an altered surface mesh.
In this paper, we present an efficient algorithm to compute a basis for
handle and tunnel loops without requiring any 3D tessellation. This
saves time considerably for large meshes making the algorithm scalable
while computing the loops on the original input mesh and not on some
refined version of it. We use the concept of the Reeb graph which
together with several key theoretical insights on linking number
provide an initial set of loops that provably constitute a handle and a
tunnel basis. We further develop a novel strategy to tighten these
handle and tunnel basis loops to make them geometrically relevant. We
demonstrate the efficiency and effectiveness of our algorithm as well
as show its robustness against noise, and other anomalies in the input.
|

|
|
Localized Delaunay Refinement for Piecewise-Smooth Complexes (full version)
T. K. Dey and A. Slatton (SoCG 2013) Proc. 29th Annu. Sympos. Comput. Geom. (2013), pages 47--56.
[software LocPSC] [Talk Slides]
The Delaunay
refinement, a versatile method of mesh generation, is plagued by memory
thrashing when required to generate large output meshes. To address
this space issue, a localized version of Delaunay refinement was
proposed for generating meshes for smooth surfaces and volumes bounded
by them. The method embodies a divide-and-conquer paradigm in that it
maintains the growing set of sample points with an octree and produces
a local mesh within each individual node, and stitches these local
meshes seamlessly. The proofs of termination and global consistency for
localized methods exploit recently developed sampling theory for smooth
surfaces. Unfortunately, these proofs break down for a larger class
called piecewise smooth complexes (PSCs) that allow smooth surface
patches that are joined along ridges and corners. In this work, we adapt a recently developed
sampling and meshing algorithm for PSCs into the localization
framework. This requires revisiting the original algorithm, and more
importantly re-establishing the correctness proofs to accommodate the
localization framework. Our implementation of the algorithm exhibits
that it can indeed generate large meshes with significantly less time
and memory than the original algorithm without localization. In fact,
it beats a state-of-the-art meshing tool of CGAL for generating large
meshes.
|

|
|
Voronoi-based Feature Curves Extraction for Sampled Singular Surfaces
T. K. Dey and L. Wang (SMI 2013), Computers & Graphics, special issue of Shape Modeling International (2013), Vol. 37 (6), 659--668.
[Web-page] [software SingularCocone]
The
detection and reconstruction of feature curves in surfaces from a point
cloud data is a challenging problem because most of the known theories
for smooth surfaces break down at these places. The features such as
boundaries, sharp ridges and corners, and curves where multiple surface
patches intersect creating non-manifold points are often considered
important geometries for further processing. As a result, they need to
be preserved in a reconstruction of the sampled surface from its point
sample. The problem becomes harder in presence of noise. We propose a
robust Voronoi-based pipeline that engages several sub steps consisting
of approaches proposed originally for smooth case. We modify or enhance
them to handle features in singular surfaces. The experimental results
provide the evidence that the method is effective.
Note: This paper extracts features differently than our ``Feature-Preserving reconstruction of singular surfaces" paper which introduced the WeightCocone to reconstruct with feature curves
|

|
|
Weighted graph Laplace operator under topological noise
T. K. Dey, P. Ranjan, and Y. Wang. (SODA 2013), ACM-SIAM Symposium on Discrete Algorithms (2013).
Recently,
various applications have motivated the study of spectral structures
(eigenvalues and eigenfunctions) of the so-called Laplace-Beltrami
operator of a manifold and their discrete versions. A popular choice for the discrete version is the so-called Gaussian
weighted graph Laplacian which can be applied to point cloud data that
samples a manifold. Naturally, the question of stability of the
spectrum of this discrete Laplacian under the perturbation of the
sampled manifold becomes important for its practical usage. Previous
results showed that the spectra of both the manifold Laplacian and
discrete Laplacian are stable when the perturbation is ``nice'' in the
sense that it is restricted to a diffeomorphism with minor area
distortion. However, this forbids, for example, small topological
changes.
We study the stability of the spectrum of the weighted graph Laplacian
under more general perturbations. In particular, we allow arbitrary,
including topological, changes to the hidden manifold as long as they
are localized in the ambient space and the area distortion is small.
Manifold Laplacians may change dramatically in this case. Nevertheless,
we show that the weighted graph Laplacians computed from two sets of
points, uniformly randomly sampled from a manifold and a perturbed
version of it, have similar spectra. The distance between the two
spectra can be bounded in terms of the size of the perturbation and
some intrinsic properties of the original manifold.
|

|
|
Animating
bubble interactions in a liquid foam
O. Busaryev, T. K. Dey, H. Wang,
and R. Zhong. (SIGGRAPH 2012), ACM Trans. Graphics, Vol. 31 (4), 2012. [Video
link]
Bubbles and foams are important features of liquid surface phenomena,
but they are difficult to animate due to their thin films and complex interactions
in the real world. In particular, small bubbles (having diameter <1cm)
in a dense foam are highly affected by surface tension, so their shapes
are much less deformable compared with larger bubbles. Under this small
bubble assumption, we propose a more accurate and efficient particle-based
algorithm to simulate bubble dynamics and interactions. The key component
of this algorithm is an approximation of foam geometry, by treating bubble
particles as the sites of a weighted Voronoi diagram. The connectivity information
provided by the Voronoi diagram allows us to accurately model various
interaction effects among bubbles. Using Voronoi cells and weights, we
can also explicitly address the volume loss issue in foam simulation, which
is a common problem in previous approaches. Under this framework, we present
a set of bubble interaction forces to handle miscellaneous foam behaviors,
including foam structure under Plateau's laws, clusters formed by liquid
surface bubbles, bubble-liquid and bubble-solid coupling, bursting and coalescing.
Our experiment shows that this method can be straightforwardly incorporated
into existing liquid simulators, and it can efficiently generate realistic
foam animations, some of which have never been produced in graphics before.
|

|
|
Feature-Preserving
reconstruction of singular surfaces
T. K. Dey, X. Ge, Q. Que, I.
Safa, L. Wang, Y. Wang. Computer Graphics Forum, Vol. 31 (5), 1787--1796,
special issue of Eurographics Sympos. Geometry Processing (SGP 2012). [Talk
slides]
Reconstructing a surface mesh from a set of discrete point samples is a
fundamental problem in geometric modeling. It becomes challenging in presence
of `singularities' such as boundaries, sharp features, and non-manifolds.
A few of the current research in reconstruction have addressed handling some
of these singularities, but a unified approach to handle them all is missing.
In this paper we allow the presence of various singularities by requiring
that the sampled object is a collection of smooth surface patches with boundaries
that can meet orintersect.
Our algorithm first identifies and reconstructs the features where singularities
occur. Next, it reconstructs the surface patches containing these feature
curves. The identification and reconstruction of feature curves are achieved
by a novel combination of the Gaussian weighted graph Laplacian and the
Reeb graphs. The global reconstruction is achieved by a method akin to the
well known Cocone reconstruction, but with weighted Delaunay triangulation
that allows protecting the feature samples with balls. We provide various
experimental results to demonstrate the effectiveness of our feature-preserving
singular surface reconstruction algorithm.
|

|
|
Topological
Persistence for circle valued maps
D. Burghelea and T. K. Dey. Discrete & Computational Geometry, Volume 50, No. 1 (2013), 69--98. Also in arXiv:1104.5646.
April, 2011.
We study circle valued maps and consider the persistence
of the homology of their fibers. The outcome is a finite collection
of computable invariants which answer the basic questions on persistence
and in addition encode the topology of the source space and its relevant
subspaces. Unlike persistence of real valued maps, circle valued maps
enjoy a different class of invariants celled Jordan cells in addition to
bar codes. We establish a relation between the homology of the source space
and of its relevant subspaces with these invariants and provide a new algorithm
to compute these invariants from an input matrix that encodes a circle
valued map on an input simplicial complex.
Also see how it all started: arXiv:1012.3763, 2010.
|

|
|
Eigen
deformation of 3D models
T. K. Dey, P. Ranjan and Y.
Wang. Proc. Computer Graphics International (CGI 2012). The Visual Computer Volume 28, Numbers 6-8 (2012), 585-595, DOI: 10.1007/s00371-012-0705-0 [Talk
slides] [Video]
Recent advances in mesh deformation
have been dominated by two techniques: one uses an interactive structure
like a cage which transfers the user intended moves to the mesh, the other
lest the user to impart the moves to the mesh directly. The former one lets
the user deform the model in real-time and also preserves the shape with
sophisticated techniques like Green Coordinates. The direct techniques on
the other hand free the user from the burden of creating an appropriate cage
though they take more computing time to solve larger non-linear optimizations.
It would be ideal to develop a cage-free technique that provides real-time
defoirmation while respecting the local geometry. Using a simple eigen-framework
we devise such a technique. Our framework creates an implicit skeleton automatically.
The user only specifies the motion in a simple and intuitive manner, and
our algorithm computes a deformation whose quality is similar to that of
the cage-based scheme with Green Coordinates.
|

|
|
Annotating
simplices with a homology basis and its applications
O. Busaryev, S. Cabello, C.
Chen, T. K. Dey, and Y. Wang. 13th Scandinavian
Sympos. Workshops Algorithm Theory (SWAT 2012).
Lecture Notes in Computer Science Volume 7357, 2012, pp 189-200.
[Talk
slides] Earlier arxiv version arXiv:1107.3793v2
Let K be a simplicial complex and g the dimension of its p-th homology
group H_p(K) defined with Z_2 coefficients. We show that we can compute
a basis H of H_p(K) and annotate each p-simplex of K with a binary vector
of length g with the following property: the annotations, summed over
all p-simplices in any p-cycle z, provide the coordinate vector of the
homology class [z] in the basis H. The basis and the annotations for all
simplices can be computed in O(n^{\omega}) time, where n is the size of
K and \omega<2.376 is a quantity so that two nxn matrices can
be multiplied in O(n^{\omega}) time. The pre-computation of annotations
permits answering queries about the independence or the triviality of p-cycles
efficiently. Using annotations of edges in 2-complexes, we derive better
algorithms for computing optimal basis and optimal homologous cycles in
1-dimensional homology. Specifically, for computing an optimal basis of
H_1(K),we improve the time complexity known for the problem from O(n^4)
to O(n^{\omega}+n^2g^{\omega-1}). Here n denotes the size of the 2-skeleton
of K and g the rank of H_1(K). Computing an optimal cycle homologous to
a given 1-cycle is NP-hard even for surfaces and an algorithm taking 2^{O(g)}n\log
n time is known for surfaces. We extend this algorithm to work with arbitrary
2-complexes in O(n^{\omega})+2^{O(g)}n^2\log n time using annotations.
Also see this technical
report for a more practical algorithm.
|

|
|
Localized
Delaunay refinement for volumes
T. K. Dey and A. G. Slatton.
Computer Graphics Forum, Vol 30 (5), 1417--1426. Special issue Proc.
of Eurographics Sympos. Geometry Processing (SGP
2011). [Web-page]
[Talk
slides] [Software]
Delaunay refinement, recognized as
a versatile tool for meshing a variety of geometries, has the deficiency
that it does not scale well with increasing mesh size. The bottleneck
can be traced down to the memory usage of 3D Delaunay triangulations.
Recently an approach has been suggested to tackle this problem for the
specific case of smooth surfaces by subdividing the sample set in an
octree and then refining each subset individually while ensuring {\em
termination} and {\em consistency}. We extend this to localized refinement
of volumes, which brings about some new challenges. We show how these
challenges can be met with simple steps while retaining provable guarantees,
and that our algorithm scales many folds better than a state-of-the-art
meshing tool provided by CGAL.
Also, see the paper
below on localized Delaunay refinement for surfaces.
|

|
|
Reeb graphs: approximation
and persistence
T. K. Dey and Y. Wang. Proc.
27th Annu. Sympos. Comput. Geom. (SOCG 2011),
226--235. Extended version in Discrete & Computational Geometry, Vol. 49 (2013), 46--73.
[Extended
version]
Given a continuous
function f: X-> R on a topological space X, its {\em level set}
f^{-1}(a) changes continuously as the real value a changes. Consequently,
the connected components in the level sets appear, disappear, split and
merge. The Reeb graph of f summarizes this information into a graph
structure. Previous work on Reeb graph mainly focused on its efficient
computation. In this paper, we initiate the study of two important aspects
of the Reeb graph which can facilitate its broader applications in
shape and data analysis. The first one is the approximation of the Reeb
graph of a function on a smooth compact manifold M without boundary. The
approximation is computed from a set of points P sampled from M. By leveraging
a relation between the Reeb graph and the so-called {\em vertical homology
group}, as well as between cycles in M and in a Rips complex constructed
from P, we compute the H_1-homology of the Reeb graph from P. It takes O(n
\log n) expected time, where n is the size of the 2-skeleton of the Rips
complex. As a by-product, when M is an orientable 2-manifold, we also
obtain an efficient near-linear time (expected) algorithm to compute the
rank of H_1(M) from point data. The best known previous algorithm for this
problem takes O(n^3) time for point data. The second aspect concerns the
definition and computation of the \emph{persistent Reeb graph homology}
for a sequence of Reeb graphs defined on a filtered space. For a piecewise-linear
function defined on a filtration of a simplicial complex K, our algorithm
computes all persistent H_1-homology for the Reeb graphs in O(n n_e^3) time,
where n is the size of the 2-skeleton and n_e is the number of edges in K.
|

|
|
Localized Delaunay
refinement for sampling and meshing. [Talk
slides][Web-page][Software]
T. K. Dey, J. A. Levine, and
A. Slatton. Computer Graphics Forum. Vol. 29 (5)(2010), 1723--1732.
Specail issue of Proc. Eurographics Sympos. Geometry Processing.
(SGP 2010).
[Extended
version]
The technique of Delaunay
refinement has been recognized as a versatile tool to generate
Delaunay meshes of a variety of geometries. Despite its usefulness,
it suffers from one lacuna that limits its application. It does
not scale well with the mesh size. As the sample point set grows,
the Delaunay triangulation starts stressing the available memory space
which ultimately stalls any effective progress. A natural solution to
the problem is to maintain the point set in clusters and run the refinement
on each individual cluster. However, this needs a careful point insertion
strategy and a balanced coordination among the neighboring clusters to
ensure consistency across individual meshes. We design an octtree based
localized Delaunay refinement method for meshing surfaces in three dimensions
which meets these goals. We prove that the algorithm terminates and provide
guarantees about structural properties of the output mesh. Experimental
results show that the method can avoid memory thrashing while computing
large meshes and thus scales much better than the standard Delaunay refinement
method.
|

|
|
Persistent
heat signature for pose-oblivious matching of incomplete models.
[Talk
slides]
T. K. Dey, K. Li, C. Luo, P.
Ranjan, I. Safa, and Y. Wang. Computer Graphics Forum. Vol.
29 (5) (2010), 1545--1554. Special isue of Proc. Sympos. Geometry
Processing. (SGP 2010).
Although understanding
of shape features in the context of shape matching and retrieval
has made considerable progress in recent years, the case for partial
and incomplete models in presence of pose variations still begs a robust
and efficient solution. A signature that encodes features at multi-scales
in a pose invariant manner is more appropriate for this case. The
Heat Kernel Signature function from spectral theory exhibits this multi-scale
property. We show how this concept can be merged with the persistent
homology to design a novel efficient pose-oblivious matching algorithm
for all models, be they partial, incomplete, or complete. We make the
algorithm scalable so that it can handle large data sets. Several
test results show the robustness of our approach.
|

|
|
Tracking
a generator by persistence.
O. Busaryev, T. K. Dey, and
Y. Wang. 16th Annu. Internat. Computating and Combinatorics
Conf. (COCOON 2010), 278--287. Journal
version in Discrete Mathematics, Algorithms and Applications, Vol
2, Issue 4, 2010, 539--552.
DOI:10.1142/S1793830910000875.
The persistent homology
provides a mathematical tool to describe ``features" in a principle
manner. The persistence algorithm proposed by Edelsbrunner et al.
[5] can compute not only the persistent homology for a filtered
simplicial complex, but also representative generating cycles for
persistent homology groups. However, if there are dynamic changes either
in the filtration or in the underlying simplicial complex, the representative
generating cycle can change wildly.
In this paper, we consider the problem of
tracking generating cycles with temporal coherence. Specifically,
our goal is to track a chosen essential generating cycle so that
the changes in it are ``local". This requires reordering simplices
in the filtration, To handle reordering operations. we build upon
the matrix framework proposed by Cohen-Steiner et al.[3] to swap
two consecutive simplices, so that we can process a reordering directly.
We present an application showing how our algorithm can track an
essential cycle in a complex constructed out of a point cloud data.
|

|
|
Optimal
homologous cycles, total unimodularity, and linear programming.
T. K. Dey, A. Hirani, and B.
Krishnamoorthy. SIAM J. Computing, Vol. 40, pp 1026--1044.
Prelim. version in 42nd ACM Sympos. Comput. Theory (STOC 2010), 221--230. arXiv:1001.0338v1[math.AT],
2nd January, 2010. [web-page]
[combined
talk-slides]
Given a simplicial
complex with weights on its simplices, and a nontrivial
cycle on it, we are interested in finding the cycle with minimal
weight which is homologous to the given one. Assuming that the
homology is defined with integer (Z) coefficients, we show the
following (Theorem 5.2):
For a finite simplicial complex K
of dimension greater than p, the boundary matrix [d_(p+1)]
is totally unimodular if and only if H_p(L,L_0) is torsion-free
for all pure subcomplexes L_0, L in K of dimension p and p+1 respectively
where L_0\subset L.
Because of the total unimodularity
of the boundary matrix, we can solve the optimization problem,
which is inherently an integer programming problem, as
a linear program and obtain integer solution. Thus the problem
of finding optimal cycles in a given homology class can be solved
in polynomial time. This result is surprising in the backdrop
of a recent result which says that the problem is NP-hard under Z_2
coefficients which, being a field, is in general easier to deal with.
One consequence of our result, among others, is that one can compute
in polynomial time an optimal 2-cycle in a given homology class for any
finite simplicial complex embedded in R^3. Our optimization approach
can also be used for various related problems, such as finding an optimal
chain homologous to a given one when they are not cycles.
|

|
|
Approximating
cycles in a shortest basis of the first homology group from point
data
T. K. Dey, J. Sun, and Y. Wang.
Inverse Problems, Vol. 27 (2011), 124004. doi:10.1088/0266-5611/27/12/124004
An earlier version appeared with title ``Approximating loops in a
shortest homology basis from point data" in Proc. 26th Annu. Sympos.
Comput. Geom. (SOCG 2010), 166--175.
arXiv:0909.5654v1[cs.CG], 30th September 2009. [web-page]
[software]
[talk-slides]
Inference
of topological and geometric attributes of a hidden manifold
from its point data is a fundamental problem arising
in many scientific studies and engineering applications. In
this paper we present an algorithm to compute a set of cycles
from a point data that presumably sample a smooth manifold M\subset
R^d. These cycles approximate a shortest basis of the one dimensional
homology group H_1(M) over coefficients in finite field Z_2.
Previous results addressed the issue of computing the rank of the
homology groups from point data, but there is no result on approximating
the shortest basis of a manifold from its point sample. In arriving
our result, we also present a polynomial time algorithm for computing
a shortest basis of H_1(K) for any finite simplicial complex K whose edges
have non-negative weights.
|

|
|
Convergence,
Stability, and Discrete Approximation of Laplace Spectra
T. K. Dey, P. Ranjan, and Y.
Wang. Proc. ACM/SIAM Sympos. Discrete Algorithms
(SODA 2010), 650--663.
Paper
with a minor correction.
Spectral
methods have been widely used in a broad range of applications
fields. One important object involved in such methods is
the Laplace-Beltrami operator of a manifold. Indeed, a variety
of work in graphics and geometric optimization uses the eigen-structures
(i.e., the eigenvalues and eigenfunctions) of the Laplace operator.
Applications include mesh smoothing, compression, editing,
shape segmentation, matching, parameterization, and so on. While
the Laplace operator is defined (mathematically) for a smooth domain,
these applications often approximate a smooth manifold by a discrete
mesh. The spectral structure of the manifold Laplcian is estimated
from some discrete Laplace operator constructed from this mesh.
In this paper, we study the important
question of how well the specturm computed from the discrete
mesh approximates the true spectrum of the manifold Lplacian.
We exploit a recent result on mesh Laplacian and provide the first
convergence result to relate the spectrum constructed from a
general mesh (approximating an m-manifold embedded in R^d) with
the true spectrum. We also study how stable these eigenvalues
and their discrete approximations are when the underlying manifold
is perturbed, and provide explicit bounds for the Laplacian spectra
of two ``close" manifolds, as well as a convergence result for their
discrete approximations. Finally, we present various experimental
results to demonstrate that these discrete spectra are both accurate
and robust in practice.
|

|
|
Repairing
and meshing imperfect shapes with Delaunay refinement
O. Busaryev, T. K. Dey, J. A.
Levine. Proc. SIAM/ACM Joint Conf. Geometric
and Physical Modeling (SPM 2009), 25--33.
As
a direct consequence of software quirks, designer errors,
and representation flaws, often three-dimensional shapes
are stored in formats that introduce inconsistencies such as
small gaps and overlaps between surface patches. We present
a new algorithm that simultaneously repairs imperfect geometry
and topology while generating Delaunay meshes of these shapes.
At the core of this approach is a meshing algorithm for input shapes
that are piecewise smooth complexes (PSCs), a collection of smooth
surface patches meeting at curves non-smoothly or in non-manifold
configuarations. Guided by a user tolerance parameter, we automatically
merge nearby components while building a Delaunay mesh that has many
of these errors fixed. Experimental evidence is provided to show
the results of our algorithm on common computer-aided design (CAD)
formats. Our algorithm may also be used to simplify shapes by
removing small features which would require an excessive number of elements
to preserve them in the output mesh.
Note: One of the main ingredients
of this paper is our PSC
meshing paper.
|

|
|
Isotopic
Reconstruction of Surfaces with Boundaries
T. K. Dey, K.
Li., E. A. Ramos, and R. Wenger. Proc.
Sympos. Geom. Processing.(SGP09), special
issue of Computer Graphics Forum, Vol. 28, No. 5 (2009),
1371--1382. [Web-page]
[Software]
[talk-slide]
[Video]
We
present an algorithm for the reconstruction of a
surface with boundaries (including a non-orientable one)
in three dimensions from a sufficiently dense sample. It is
guaranteed that the output is isotopic to the unknown sampled
surface. No previously known algorithm guarantees isotopic or homeomorphic
reconstruction of surfaces with boundaries. Our algorihtm is
surprisingly simple. It `peels' slivers greedily from an alpha-complex
of a sample of the surface. No other post-processing is necessary.
We provide several experimental results from an implementation
of our basic algorithm and also a modified version of it.
|

|
|
Cut
Locus and Topology from Surface Point Data.
T. K. Dey, K.
Li. Proc. 25th Ann. Sympos. Comput. Geom.(SOCG09), 2009, 125--134.
A
cut locus of a point in a compact Riemannian manifold
M is defined as the set of points where minimizing geodesics
issued from p stop being minimizing. It is known that a cut
locus contains most of the topological information of M.
Our goal is to utilize this property of cut loci to decipher
the topology of M from a point sample. Recently it has been shown
that Rips complexes can be built from a point sample P of
M systematically to compute the Betti numbers, the rank of the homology
groups of M. Rips complexes can be computed easily and therefore are
favored over others such as restricted Delaunay, alpha, Cech, and
witness complex. However, the sizes of the Rips complexes tend to
be large. Since the dimension of a cut locus is lower than that of
the manifold M, a subsample of P approximating the cut locus is usually
much smaller in size and hence admits a relatively smaller Rips
complex.
In this paper we explore
the above approach for point data sampled from surfaces
embedded in any high dimensional Euclidean space. We present
an algorithm that computes a subsample P' of a sample
P of a 2-manifold where P' approximates a cut locus. Empirical
results show that the first Betti number of M can be computed
from Rips complexes built on these subsamples. The sizes of
these Rips complexes are much smaller than the one built on
the original sample of M.
Our first attempt on
a related topic was the following paper:
Topology
from Data via Geodesic Complexes. T. K.
Dey and K. Li. Tech Report OSU-CISRC-3/09-TR05.
|

|
|
Delaunay
meshing of piecewise smooth complexes without
expensive predicates.
T. K. Dey, J.
A. Levine. Algorithms, vol. 2, issue 4 (2009), 1327--1349.
doi:10.3390/a2041327
Tech Report,
OSU-CISRC-7/08-TR40, July 2008.
[Video][Software][Talk-slide][Web-page]
Recently a
Delaunay
refinement algorithm has been proposed that
can mesh piecewise smooth complexes which include
polyhedra, smooth and piecewise smooth surfaces, and
non-manifolds. However, this algorihtm employs domain dependent
numerical predicates, some of which could be computationally
expensive and hard to implement. In this paper we develop a
refinement strategy that eliminates these complicated domain
dependent predicates. As a result we obtain a meshing algorithm
that is practical and implementation-friendly.
|

|
|
Persistence-based
Handle and Tunnel Loops Computation Revisited
for Speed Up.
T. K. Dey and
K. Li. Shape Modeling International (SMI09), 2009. Special issue of Computer
& Graphics, Article in press,
doi:10.1016/j.cag.2009.03.008.
[Software]
Loops in surfaces
associated with topological features such as handles and
tunnels are important entities in many applications including
surface parameterization, feature identification, and
topological simplification. Recently, a persistent homology
based algorithm has been proposed to compute them. The algorithm
has several advantages including its simplicity, combinatorial
nature and independence from computing other extra structures.
In this paper, we propose changes to this loop computation
algorithm based on some novel observations. These changes reduce
the computation time of the algorithm dramatically. In particular,
our experimental results show that the suggested changes achieve
considerable speed up for large data sets without sacrificing
loop qualities.
Note: This is a follow-up
paper of our
SIGGRAPH08 paper below.
|

|
|
Computing
Geometry-aware Handle and Tunnel Loops in 3D
Models.
T. K. Dey, K.
Li, J. Sun, and D. Cohen-Steiner. SIGGRAPH 2008, 45:1--45:9.
[Video][Software][Talk-slide][Web-page]
Many applications
such as topology repair, model editing, surface parameterization,
and feature recognition benefit from computing loops on
surfaces that wrap around their `handles' and `tunnels'.
Computing such loops while optimizing their geometric lengths
is difficult. On the other hand, computing such loops without
considering geometry is easy but may not be very useful. In this
paper we strike a balance by computing topologically correct
loops that are also geometrically relevant. Our algorithm is a
novel application of the concepts from topological persistence
introduced recently in computational topology. The usability
of the computed loops is demonstrated with some examples in feature
identification and topology simplification.
Note: See the paper
below On
computing handle and tunnel loops for
our first attempt on this problem.
|

|
|
Recursive
geometry of the flow complex
and topology of the flow complex filtration.
K. Buchin, T. K. Dey, J. Giesen, and
M. John. Comput. Geom. Theory Application. (2008),
vol. 40, 115--157.
The flow complex
is a geometric structure, similar to the Delaunay tessellation,
to organize a set of (weighted) points in R^k. Flow
shapes are topological spaces correspoding to substructures
of the flow complex. The flow complex and flow shapes
have found applications in surface reconstruction, shape
matching, and molecular modeling. In this article we give
an algorithm for computing the flow complex of weighted points
in any dimension. The algorithm reflects the recursive
structure of the flow complex. On the basis of the algorithm we
establish a topological similarity between flow shapes and the
nerve of a corresponding ball set, namely homotopy equivalence.
This paper grew out of:
Alpha-Shapes and Flow Shapes are Homotopy
Equivalent. T. K. Dey, J. Giesen and M. John. Proceedings
of the 35th Annual ACM Symposium on Theory of Computing (STOC 2003) 493-502
|
|
|
Normal
variation with adaptive feature size
(2007)
The proof of
the normal variation lemma (Lemma 2) in Amenta-Bern
paper ``Surface reconstruction by Voronoi filtering",
DCG, 1999, pg. 481-504, is not correct (which also appears
in my book on reconstruction). In this short note we fix
the problem and improve the bound on the normal variation.
This should improve various bounds derived afterwards using
the normal variation result.
|
|
|
Maintaining
Deforming Surface Meshes
S.-W. Cheng and T. K. Dey. Proc.
19th ACM-SIAM Sympos. Discrete Algorithms (SODA 2008) (2008), 112--121.
We present a method to maintain a mesh approximating
a deforming surface, which is specified by
a dense set of sample points. We identify a reasonable
motion model for which a provably good surface mesh
can be maintained. Our algorithm determines the appropriate
times at which the mesh is updated to maintain a good approximation.
The updates use simple primitives, and no costly computation
such as line-surface intersection is necessary. Point
insertions and deletions are allowed at the updates. Each
update takes time linear in the size of the current sample set
plus the new sample points inserted. We also construct examples
for which, under the same model, no other algorithm makes asymptotically
fewer changes to the mesh than our algorithm.
This paper is based on the following flip paper available
as a preprint from computational geoemtry
arxiv.
|

|
|
Delaunay
Edge Flips in Dense Surface Triangulations
S.-W. Cheng and T. K. Dey. Pre-print
arXiv:cs.CG/0712.1959, 2007. short
version in EuroCG 2008.
Note: We are retracting this result due to a bug in a Lemma (Lemma
3.1). We are trying to salvage the other results without using Lemma
3.1. The abstract was:
Delaunay
flip is an elegant, simple tool to convert
a triangulation of a point set to its Delaunay
triangulation. The technique has been researched extensively
for full dimensional triangulations of point sets. However,
an important case of triangulations which are not full
dimensional is surface triangulations in three dimensions.
In this paper we address the question of converting a surface
triangulation to a subcomplex of the Delaunay triangulation
with edge flips. We show that the surface triangulations
which closely approximate a smooth surface with uniform density
can be transformed to a Delaunay triangulation with a simple
edge flip algorithm. The condition on uniformity becomes less
stringent with increasing density of the triangulation. If the
condition is dropped completely, the flip algorithm still terminates
although the output surface triangulation becomes ``almost Delaunay"
instead of exactly Delaunay.
|
|
|
A
practical Delaunay meshing algorithm for a large
class of domains
S.-W. Cheng, T. K. Dey, and J. A. Levine.
Proc. 16th Internat. Meshing Roundtable
(IMR 2007), 477--494.
[Talk
slides]
Recently
a Delaunay refinement algorithm has been
proposed that can mesh domains as general as piecewise
smooth complexes [CDR07]. In this paper we introduce
a novel modification of the algorithm to make
it implementable in practice. In particular, we replace
four tests of the original algorithm with only a single test
that is easy to implement. The algorithm has the following
guarantees. The output mesh restricted to each manifold element
in the complex is a manifold with proper incidence relations.
More importantly, with increasing level of refinement which
can be controlled by an input parameter, the output mesh becomes
homeomorphic to the input while preserving all input features. Implementation
results on a disparate array of input domains are presented to corroborate
our claims.
For the theory see the following paper:
Theory
of a practical Delaunay meshing algorithm for a large
class of domains. S.-W. Cheng, T. K. Dey and
J. Levine. Algorithms, Architecture and Information Systems
Security, B. Bhattacharya, S. Sur-Kolay, S. Nandy and A. Bagchi
(eds.), World Scientific Review Volume 3, 2008, 17--41.
|

|
|
On
computing handle and tunnel loops
T. K. Dey, K. Li, and J. Sun.
IEEE Proc. Internat. Conf. Cyberworlds (NASAGEM workshop) (2007), 357--366.
Journal version is in Computer-Aided Design, in press,
doi:10.1016/j.cad.2009.01.001.
[Talk
slides] HandleTunnel
software
Many applications seek to identify features
like `handles' and `tunnels' in a shape bordered
by a surface embedded in three dimensions. To this end
we define handle and tunnel loops on surfaces which
can help identifying these features. We show that a closed
surface of genus g always has g handle and g tunnel loops
induced by the embedding. For a class of shapes that
retract to graphs, we characterize these loops by a linking
condition with these graphs. These characterizations lead
to algorithms for detection and generation of these loops.
We provide an impementation with applications to feature detection
and topology simplification to show the effectiveness of
the method.
|

|
|
Stability of critical points with interval persistence
T. K. Dey and R. Wenger. Discrete
& Computational Geometry, vol 38 (2007),
479--512. Tech Report OSU-CISRC-4/06-TR47, April
2006.
Scalar functions defined on a topological
space T are at the core of many applications
such as shape matching, visualization, and physical
simulations. Topological persistence is an approach
to characterizing these functions. It measures
how long topological structures in the level sets
{x in T : f(x) <= c} persist as c changes. Recently it
was shown that the critical values defining a topological
structure with relatively large persistence remain
almost unaffected by small perturbations. This result suggests
that topological persistence is a good measure for matching
and comparing scalar functions. We extend these results
to critical points in the domain
by redefining persistence and critical points and replacing
sub-level sets {x in T : f(x) <= c} with interval
sets {x in T : a<=f(x)< b}. With these modifications
we establish a stability result for critical points.
This result is strengthened for maxima that can be used
for matching two scalar functions.
|

|
|
Delaunay meshing of isosurfaces
T. K. Dey and J. A. Levine. Proc.
Shape Modeling International (SMI 2007), 241--250.
DelIso software
We present an isosurface meshing algorithm DelIso, based
on the Delaunay refinement paradigm. This paradigm
has been successfully applied to mesh a variety of domains with
guarantees for topology, geometry, mesh gradedness, and
triangle shape. A restricted Delaunay triangulation, dual
of the intersection between the surface and the three dimensional
Voronoi diagram, is often the main ingredient in Delaunay refinement.
Computing and storing three dimensional Voronoi/Delaunay
diagrams become bottlenecks for Delaunay refinement techniques
since isosurface computations generally have large input
datasets and output meshes. A highlight of our algorithm is
that we find a simple way to recover the restricted Delaunay
triangulation of the surface without computing the full 3D
structure. We employ techniques for efficient ray tracing of
isosurfaces to generate surface sample points, and demonstrate
the effectiveness of our implementation on a variety of volume
datasets. |

|
|
Delaunay refinement for piecewise
smooth complexes
S.-W. Cheng, T. K. Dey, and E. A. Ramos.
Proc. 18th Annu. ACM-SIAM Sympos.
Discrete Algorithms (SODA 2007),
1096--1105. Journal Version in Discrete &
Comput. Geom., 2008, article in press. doi.10.1007/s00454-008-9109-3.
Extended
Full Version
We present a Delaunay refinement algorithm for
meshing a piecewise smooth complex in three dimensions
with correct topology. The small angles between
the tangents of two meeting manifold patches pose difficulty.
We protect these regions with weighted points. The
weights are chosen to mimic the local feature size and to
satisfy a Lipschitz-like property. A Delaunay refinement
using the weighted Voronoi diagram is shown to terminate
with the recovery of the topology of the input. To this end,
we present new concepts and results including a new definition
of local feature size and a proof for a generalized topological
ball property.
|

|
|
Defining
and computing curve-skeletons
with medial geodesic function
T. K. Dey and J. Sun. Proc.
Sympos. Geometry Processing (SGP 2006), 143--152.
CurveSkel Software
Many applications in geometric modeling,
computer graphics, visualization, and computer
vision benefit from a reduced representation
called curve-skeletons of a shape. These are curves
possibly with branches which compactly represent
the shape geometry and topology. The lack of a proper
mathematical definition has been a bottleneck in
developing and applying the curve-skeletons. A set of desirable
properties of these skeletons has been identified and
the existing algorithms try to satisfy these properties
mainly through a procedural definition. We define a function
called medial geodesic on the medial axis which leads to
a mathematical definition and an approximation algorithm for
curve-skeletons. Empirical study shows that the algorithm
is robust against noise, operates well with a single user parameter,
and produces curve-skeletons with the desirable properties. Moreover,
the curve-skeletons can be associated with additional attributes
that follow naturally from the definition. These attributes
capture shape eccentricity, a local measure of how far a shape
is away from a tubular one.
|

|
|
Identifying
flat and tubular regions of a
shape by unstable manifolds
S. Goswami, T. K. Dey, and C. Bajaj.
Proc. 11th ACM Sympos. Solid
Modeling Applications (SPM 2006),
27--37.
We present an algorithm
to identify the flat and tubular regions of a
three dimensional shape from its point sample. We
consider the distance function to the input point cloud
and the Morse structure induced by it on R^3. Specifically
we focus on the index 1 and index 2 saddle points and their
unstable manifolds. The unstable manifolds of index
2 saddles are one dimensional whereas those of index 1 saddles
are two dimensional. Mapping these unstable manifolds
back onto the surface, we get the tubular and flat regions.
The computations are carried out on the Voronoi diagram
of the input points by approximating the unstable manifolds
with Voronoi faces. We demonstrate the performance of our
algorithm on several point sampled objects.
|

|
|
Normal
and feature approximations
from noisy point clouds.
T. K. Dey and J.
Sun. Proc. FST&TCS
2006, LNCS 4337, 21--32.
NormFet
software
We consider the problem of approximating
normal and feature sizes approximations
of a surface from point cloud data that may be
noisy. These problems are central to many applications
dealing with point cloud data. In the noise-free case,
the normals and feature sizes can be approximated
by the centers of a set of unique large Delaunay balls
called polar balls. In presence of noise, polar balls
do not necessarily remain large and hence their centers
may not be good for normal and feature approximations.
Earlier works suggest that some large Delaunay balls can play
the role of polar balls. However, these results were short
in explaining how the big Delaunay balls should be chosen for
reliable approximations and how the approximation error
depends on various factors. We provide new analyses that fill
these gaps. In particular, they lead to new algorithms for practical
and reliable normal and feature approximations.
|

|
|
Anisotropic
surface meshing
S.-W. Cheng, T. K. Dey and E. A. Ramos.
Proc. ACM-SIAM Sympos. Discrete
Algorithms (SODA 2006), 202--211.
We study the problem
of triangulating a smooth closed implicit
surface S endowed with a 2D metric tensor that varies
over S. This is commonly known as the anisotropic
surface meshing problem. We extend the 2D metric tensor
naturally to 3D and employ the 3D anisotropic Voronoi
diagram of a set P of samples on S to triangulate S. We
prove that a restricted dual, Mesh P, is a valid
triangulation homeomorphic to S under appropriate conditions.
We also develop an algorithm for constructing P and
Mesh P. In addition to being homeomorphic to S,
each triangle in Mesh P is well-shaped when measured using
the 3D metric tensors of its vertices. Users can set upper
bounds on the anisotropic edge lengths and the angles between
the surface normals at vertices and the normals of incident
triangles (measured both isotropically and anisotropically).
|
|
|
An Adaptive MLS Surface for
Reconstruction with Guarantees.
T. K. Dey and J.
Sun. Symposium on
Geometry Processing (SGP 2005),
43--52.
Conference
version.
Extended
version.
Technical
Report OSU-CISRC-4-05-TR26, April, 2005.
AMLS Software
Recent work have
shown that moving least squares (MLS) surfaces
can be used effectively to reconstruct surfaces
from possibly noisy point cloud data. Several
variants of MLS surfaces have been suggested, some
of which have been analyzed theoretically for guarantees.
These analyses, so far, have assumed uniform sampling
density. We propose a new variant of the MLS surface
that, for the first time, incorporates local feature sizes
in its formulation, and we analyze it for reconstruction
guarantees using a non-uniform sampling density. The
proposed variant of the MLS surface has several computational
advantages over existing MLS methods.
Also see
Extremal
Surface Based Projections
Converge and Reconstruct with Isotopy.
T. K. Dey, S. Goswami and
J. Sun. Technical Report
OSU-CISRC-05-TR25, April, 2005.
An early attempt
T. K. Dey, S. Goswami and
J. Sun. Smoothing
noisy point clouds
with Delaunay preprocessing and MLS.
Tech-report OSU-CISRC-3/04-TR17, 2004.
|

|
|
Normal
Estimation for Point
Clouds : A Comparison Study for a
Voronoi Based Method
T. K. Dey, G. Li
and J. Sun. Eurographics Sympos.
on Point-Based Graphics (2005), 39--46.
Many applications that process
a point cloud data benefit from a reliable
normal estimation step. Given a point cloud presumably
sampled from an unknown surface, the problem
is to estimate the normals of the surface at the
data points. Two approaches, one based on numerical
optimizations and another based on Voronoi diagrams are
known for the problem. Variations of numerical approaches
work well even when point clouds are contaminated with
noise. Recently a variation of the Voronoi based method is proposed
for noisy point clouds. The centrality of the normal
estimation step in point cloud processing begs a thorough
study of the two approaches so that one knows which approach
is appropriate for what circumstances. This paper presents
such results.
|

|
|
Polygonal Surface
Remeshing with Delaunay Refinement
T. K. Dey, G. Li
and T. Ray. Proc.14th Internat.
Meshing Roundtable, (IMR
2005), 343--361.
Journal version in Engineering with Computers, vol. 26,
page 289--301, 2010.
Conference
version
Extended
version
SurfRemesh
software
Polygonal meshes are used
to model smooth surfaces in many applications.
Often these meshes need to be remeshed for
improving the quality, density or gradedness.
We apply the Delaunay refinement paradigm to design
a provable algorithm for isotropic remeshing of a
polygonal mesh that approximates a smooth surface.
The proofs provide new insights and our experimental
results corroborate the theory.
|

|
|
Weighted
Delaunay Refinement
for Polyhedra with Small Angles
S.-W. Cheng, T. K.
Dey and T. Ray. Proc.14th
Internat. Meshing Roundtable (IMR 2005), 325--342.
Recently, a provable Delaunay
meshing algorithm called QMesh has been
proposed for polyhedra that may have acute input
angles. The algorithm guarantees bounded circumradius
to shortest edge length ratio for all tetrahedra
except the ones near small input angles. This guarantee
eliminates or limits the occurrences of all types
of poorly shaped tetrahedra except slivers. A separate
technique called weight pumping is known for sliver
elimination. But, allowable input for the technique
so far have been periodic point sets and piecewise linear
complex with non-acute input angles. In this paper, we
incorporate the weight pumping method into QMesh thereby
ensuring that all tetrahedra except the ones near small
input angles have bounded aspect ratio. Theoretically,
the algorithm has an abysmally small angle guarantee inherited
from the weight pumping method. Nevertheless, our experiments
show that it produces better angles in practice.
|

|
|
Critical points of distance
to an epsilon-sampling of a surface and flow-complex- based surface reconstruction.
T. K. Dey, J. Giesen,
E. A. Ramos and B. Sadri.
Proc. 21st Annu. Sympos. Comput.
Geom., (SOCG 2005), 218--227.
( Invited Journal version in Internat.
J. Comput. Geom. Applications, Vol 18, 2008, 29--61.)
Extended
version.
The distance function
to surfaces in three dimensions plays
a key role in many geometric modeling applications
such as medial axis approximations, surface
reconstructions, offset computations, feature
extractions and others. In most of these cases,
the distance function to the surface is approximated
by a discrete distance function where the distances
are measured from a discrete sample of the surface.
The critical points of the distance function determines
the topology of the geometric structures in question.
Howvere, no theoretical result exists linking the
sampling and the critical point structures of the distance
functions. We provide this link by showing that the critical
points of the discrete distance function either lie very
close to the surface or near the medial axis both quantified
with the sampling density. One implication of this result
is that known Morse theory based surface reconstruction
algorithms do indeed approximate the surface geometrically.
|

|
|
Manifold
Reconstruction from Point Samples
Siu-Wing Cheng,
T. K. Dey and E. A. Ramos. Proc.
ACM-SIAM Sympos. Discrete Algorithms, (SODA 2005), 1018--1027.
Extended
AbstractSee
also [Talk
slides]
We present an algorithm
to "reconstruct" a smooth k-dimensional
manifold M embedded in an Euclidean
space R^d from a "sufficiently dense" point sample
from the manifold. The algorithm outputs a
simplicial manifold that is homeomorphic and
geometrically close to M. The running time is O(nlogn)
where n is the number of points in the sample (the
multiplicative constant depends exponentially on the
dimension though). |

|
|
Delaunay
Triangulations Approximate
Anchor Hulls
T. K. Dey, Joachim
Giesen and Samrat Goswami. Comput. Geom. Theory
Applications, vol. 36 (2006), 131--143. (prelim.
version in (SODA 2005), 1028-1037).
Recent results establish
that a subset of the Voronoi diagram
of a point set that is sampled from a smooth
boundary of a shape approximates the medial
axis. The corresponding question for the dual Delaunay
triangulation is not addressed in the literature.
We show that, for two dimensional shapes, the
Delaunay triangulation approximates a specific
structure which we call anchor hulls.
As an application we demonstrate that our approximating
result is useful for the problem of shape matching.
|

|
|
Quality
meshing for polyhedra with small angles
S.-W. Cheng, T. K.
Dey, E. Ramos and T. Ray. International
J. Comput. Geom. & Applications, Vol. 15,
No. 4 (2005), 421--461. Prelim. version in (SOCG 2004).
Extended
version
QualMesh Software
We present an algorithm
to compute a Delaunay mesh conforming
to a polyhedron possibly with small input
angles. The radius-edge ratio of most output
tetrahedra are bounded by a constant, except possibly
those that are provably close to small angles. Further,
the mesh is graded, that is, edge lengths are at
least a constant fraction of the local feature
sizes at the edge endpoints. Unlike a previous algorithm,
this algorithm is simple to implement as it avoids
computing local feature sizes and protective zones
explicitly. Our experimental results confirm our claims
and show that few skinny tetrahedra remain.
|

|
|
Sampling
and meshing a surface with guaranteed topology
and geometry
S.-W. Cheng, T. K.
Dey, E. Ramos and T. Ray.Proc. 20th
Sympos. Comput. Geom. (SOCG 2004),
280--289 .
Extended
version,
in SIAM Journal Computing, Vol. 37 (2007), 1199--1227.
This paper presents
an algorithm for sampling and triangulating
a smooth surface in R3 where
the triangulation is homeomorphic to the
surface. The only assumption we make is that the
input surface representation is amenable
to certain types of computations, namely computations
of the intersection points of a line with the surface,
computations of the critical points of some
height functions defined on the surface and its restriction
to a plane, and computations of some silhouette points.
The algorithm ensures bounded aspect ratio, size optimality,
and smoothness of the output triangulation. Unlike
previous algorithms, this algorithm does not need
to compute the local feature size for generating the sample
points which was a major bottleneck. Experiments show
the usefulness of the algorithm in remeshing and meshing
CAD surfaces that are piecewise smooth.
|

|
|
Provable
surface reconstruction from
noisy samples
T. K. Dey and S.
Goswami. Computationa
Geometry Theory & Applications, vol. 35,
2006, 124--141. Prelim. version
in (SOCG 2004).
RobustCocone
software
We present an
algorithm for surface reconstruction
in presence of noise. We show that, under a reasonable
noise model, the algorithm has theoretical
guarantees. Actual performance of the algorithm
is illustrated by our experimental results.
|

|
|
Approximating
the Medial Axis
from the Voronoi Diagram with a Convergence
Guarantee
T. K. Dey and W.
Zhao. Algorithmica, vol.
38, 2003, 179--200.
Medial Software
The medial axis
of a surface in 3D is the closure of all points
that have two or more closest points on
the surface. It is an essential geometric structure
in a number of applications involving 3D geometric
shapes. Since exact computation of the medial
axis is difficult in general, efforts continue to
improve their approximations. Voronoi diagrams turn out
to be useful for this approximation. Although it is known
that Voronoi vertices for a sample of points from a
curve in 2D approximate its medial axis, similar result
does not hold in 3D. Recently, it has been discovered
that only a subset of Voronoi vertices converge to the
medial axis as sample density approaches infinity. However,
most applications need a non-discrete approximation as
opposed to a discrete one. To date no known algorithm can
compute this approximation straight from the Voronoi
diagram with a guarantee of convergence.We present
such an algorithm and its convergence analysis in this
paper. One salient feature of the algorithm is that it is
scale and density independent. Experimental results
corroborate our theoretical claims.
|

|
|
Hierarchy
of surface models
and irreducible triangulation
S.-W. Cheng, T. K.
Dey and S.-H. Poon.Computational
Geometry : Theory & Applications, Vol. 27, No.
2 (2004), 135--150
Given a triangulated
closed surface, the problem of constructing
a hierarchy of surface models of decreasing
level of detail has attracted much attention
in computer graphics. A hierarchy provides
a view-dependent refinement and facilitates the computation
of parameterization. For a triangulated closed
surface of n vertices and genus g, we prove that there is
a constant c>0 such that if n > c g, a greedy strategy
can identify \Theta(n) topology-preserving edge contractions
that do not interfere with each other. Further, each
of them affects only a constant number of triangles. Repeatedly
identifying and contracting such edges produces
a topology-preserving hierarchy of O(n+g^2) size and O(logn
+g) depth. Although several implementations exist
for constructing hierarchies, our work is the first
to show that a greedy algorithm can efficiently compute
a hierarchy of provably small size and low depth. When no
contractible edge exists, the triangulation is irreducible.
Nakamoto and Ota showed that any irreducible triangulation
of an orientable 2-manifold has at most max{342g-72,
4} vertices. Uisng our proof techniques we obtain
a new bound of mx{240g,4}. |

|
|
Shape segmentation
and matching with flow discretization
T. K. Dey, J. Giesen
and S. Goswami. Proc. Workshop Algorithms
Data Strucutres (WADS 03),
LNCS 2748, F. Dehne, J.-R. Sack, M. Smid Eds.,
25--36
Extended
version
Segmatch Software
Geometric shapes
are identified with their features. For computational
purposes a concrete mathematical definition
of features is required. In this paper
we use a topological approach, namely dynamical
systems, to define features of shapes. To exploit
this definition algorithmically we assume
that a point sample of the shape is given as input
from which features of the shape have to be
approximated. We translate our definition
of features to the discrete domain while mimicking
the set-up developed for the continuous shapes.
The outcome of this approach is a clean mathematical
definition of features that are efficiently computable
with combinatorial algorithms. Experimental results
show that our algorithms segment shapes in two and
three dimensions into so-called features quite effectively.
Further, we develop a shape matching algorithm that
takes advantage of our robust feature segmentation
step. Performance of this algorithm is exhibited with
experimental results.
Also see the following
paper:
Shape
segmentation and
matching from noisy point clouds
T. K. Dey, J. Giesen
and S. Goswami. Proc. Eurographics Sympos.
Point-Based Graphics (2004), Marc Alexa
and S. Rusinkiewicz (eds) (2004), 193--199.
|

|
|
Quality
meshing with weighted
Delaunay refinement
S.-W. Cheng and
T. K. Dey.SIAM J. Computing, Vol. 33 (2003),
69--93 Preliminary version
in (SODA 2002).
Delaunay meshes
with bounded circumradius to shorten edge
length ratio have been propsed in the past
for quality meshing. The only poor quality
tetrahedra called slivers
that can occur in such a mesh can be eliminated
by the sliver exudation method.
This method has been shown to work for periodic
point sets, but not with boundaries. Recently a randomized
point-placement strategy has been proposed
to remove slivers while conforming to a given boundary.
In this paper we present a deterministic algorithm
for generating a weighted Delaunay mesh which respects
the input boundary and has no poor quality tetrahedron
including slivers. As in previous work, we assume that
no input angle is acute. This success is achieved
by combining the weight pumping method for sliver exudation
and the Delaunay refinement method for boundary conformation.
|

|
|
Shape
dimension and approximation
from samples
T. K. Dey, J. Giesen,
S. Goswami and W. Zhao. Discrete
& Comput. Geom., vol 29, 419--434
(2003) Prelim. version in (SODA 2002).
There are many scientific
and engineering applications where
an automatic detection of shape dimension from
sample data is necessary. Topological dimensions
of shapes constitute an important global
feature of them. We present a Voronoi based dimension
detection algorithm that assigns a dimension
to a sample point which is the topological dimension
of the manifold it belongs to. Based on this dimension
detection, we also present an algorithm to approximate
shapes of arbitrary dimension from their samples.
Our empirical results with data sets in three dimensions
support our theory. |

|
|
A
simple algorithm
for homeomorphic surface reconstruction
N. Amenta, S. Choi,
T. K. Dey and N. Leekha.
Intl. Journal on Computational
Geometry & Applications, vol. 12, (2002), 125--141.
Prelim. version in (SOCG 2000).
The problem of computing
a piecewise linear approximation to
a surface from a set of sample points is improtant
in solid modeling, computer graphics
and computer vision. A recent algorithm using
the Voronoi diagram of the sample points gave
a guarantee on the distance of the output surface
from the original sampled surface assuming that
the sample was sufficiently dense. We give a
similar algorithm, simplifying the computation and the
proof of the geometric guarantee. In addition, we guarantee
that our output surface is homeomorphic to the original
surface; to our knowledge this is the first such topological
guarantee for this problem.
Also see the following
paper:
Tight
Cocone : A water-tight
surface reconstructor
T. K. Dey and S. Goswami. J. Computing
Inform. Sci. Engin., vol. 30, (2003),
302--307.
Cocone Software
|

|
|
Dynamic
skin triangulation
H-L. Cheng, T. K.
Dey, H. Edelsbrunner and J. Sullivan.
Discrete Comput. Geom., vol.
25, (2001), 525--568 Prelim. version
in (SODA 2001).
This paper describes
an algorithm for maintaining an approximating
triangulation of a deforming
surface in R 3 . The surface is the envelope
of an infinite family of spheres defined and
controlled by a finite collection of weighted points.
The triangulation adapts dynamically to changing
shape, curvature, and topology of the surface.
|

|
|
Sliver
exudation
S.-W. Cheng, T. K.
Dey, H. Edelsbrunner, M. A. Facello and
S.-H. Teng.J. ACM, Vol. 47, (2000), 883--904
Prelim. version in (SOCG 1999).
A sliver is a tetrahedron
whose four vertices lie close to a
plane and whose orthogonal projection to that
plane is a convex quadrilateral with
no short edge. Slivers are notoriously common
in 3-dimensional Delaunay triangulations even
for well-spaced point sets. We show that if the
Delaunay triangulation has the ratio property
then there is an assignment of weights so the
weighted Delaunay triangulation contains no
slivers. We also give an algorithm to compute such
a weight assignment. |

|
|
A
simple provable
algorithm for curve reconstruction
T. K. Dey and P.
Kumar.Proc. 10th. ACM-SIAM Symposium
on Discrete Algorithms (SODA '99)
, 1999, 893--894
We present an algorithm
that provably reconstructs a curve in
the framework introduced by Amenta, Bern and
Eppstein. The highlights of the algorithm
are: (i) it is simple, (ii) it requires a sampling
density better than previously known, (iii)
it can be adapted for curve reconstruction
in higher dimensions straightforwardly.
|

|
|
Topology
preserving edge
contraction
T. K. Dey, H. Edelsbrunner,
S. Guha and D. Nekhayev.Publications
de l' Institut Mathematique (Beograd), Vol.
60 (80), 23--45, 1999
We study edge contractions
in simplicial complexes and local
conditions under which they preserve the
topological type. The conditions are
based on a generalized notion of boundary, which
lends itself to defining a nested hierarchy
of triangulable spaces measuring the distance to
being a manifold. |

|
|
Transforming
curves on surfaces
T. K. Dey and S.
Guha.Journal of Computer and System
Sciences, vol. 58, 1999, 297--325. Preliminary
version in IEEE (FOCS 1995),
266-274
We describe an optimal
algorithm to decide if one closed curve
on a triangulated 2-manifold can be continuously
transformed to another, i.e., if they are
homotopic. Suppose C_1 and C_2 are two closed curves
on a surface M of genus g. Further, suppose T is a
triangulation of M of size n such that C_1 and C_2 are
represented as edge-vertex sequences of lengths k_1 and
k_2 in T, respectively. Then, our algorithm decides
if C_1 and C_2 are homotopic in O(n+k_1+k_2) time and
space, provided g \not = 2 if M is orientable, and g \not
3, 4 if M is non-orientable. This as well implies an
optimal algorithm to decide if a closed curve on a surface
can be continuously contracted to a point. Except
for the three low genus cases, our algorithm completes
an investigation into the computational complexity of two
classical problems for surfaces posed by the mathematician
Max Dehn at the beginning of this century. The novelty
of our approach is in the application of methods from
modern combinatorial group theory.
Reprint available
upon request |

|
|
Improved
bounds for planar
k-sets and related problems
T. K. Dey.Invited
paper in a special issue of Discrete
& Computational Geometry, Vol. 19,
No. 3, (1998), 373-382
Prelim. version in IEEE (FOCS 1997).
We prove an O(nk1/3)
upper bound for planar k-sets.
This is the first considerable improvement
on this bound after its early solutions
approximately twenty seven years ago. Our proof
technique also applies to improve the current
bounds on the combinatorial complexities of k-levels
in arrangements of line segments, k convex polygons
in the union of n lines, parametric minimum spanning
trees and parametric matroids in general.
|

|
|
Extremal
problems for geometric
hypergraphs
T. K. Dey and J.
Pach.Discrete & Computational Geometry,
Vol. 19, No. 4, (1998), 473--484. Preliminary
version in ISAAC 96, LNCS
1178, 105-114
A geometric hypergraph
H is a collection of i-dimensional simplices,
called hyperedges or, simply, edges,
induced by some (i + 1)-tuples of a vertex set
V in general position in d-space. The topological
structure of geometric graphs, i.e., the case
d = 2; i = 1, has been studied extensively, and
it proved to be instrumental for the solution of a
wide range of problems in combinatorial and computational
geometry. They include the k-set problem, proximity
questions, bounding the number of incidences
between points and lines, designing various efficient
graph drawing algorithms, etc. In this paper, we
make an attempt to generalize some of these tools to
higher dimensions. We will mainly consider extremal
problems of the following type. What is the largest number of
edges (i-simplices) that a geometric hypergraph of
n vertices can have without containing certain forbidden
configurations? In particular, we discuss the special
cases when the forbidden configura tions
are k intersecting edges, k pairwise intersecting edges,
k crossing edges, k pairwise crossing edges, k edges
that can be stabbed by an i-flat, etc. Some of our estimates
will be tight. |
|
|
Computational
Topology
T. K. Dey, H. Edelsbrunner
and S. Guha. Advances in Discrere
and Computational Geometry, eds. B. Chazelle,
J. E. Goodman and R. Pollack. Contemporary
Mathematics, AMS, Providence, 1998 .
The authors of this
article believe there is or should be a
research area appropriately referred to as
computational topology. Its agenda includes
the identification and formalization of
topological questions in computer applications
and the study of algorithms for topological
problems. It is hoped this article can contribute
to the creation of a computational branch
of topology with a unifying influence on computing
and computer applications. |

|
|
Visibility
with multiple reflections
B. Aronov, A. Davis,
T. K. Dey, S. P. Pal and D. C. Prasad.Discrete
& Computational Geometry, Vol.
20, No. 61, (1998), 61--78. Preliminary
version in 5th SWAT, 1996,
LNCS 1097, 284-295
We show that the
region lit by a point light source inside
a simple n-gon after at most k reflections
off the boundary has combinatorial complexity
O(n2k ), for any k – 1. A lower bound
of Ω((n/k θ(1))2k ) is also established
which matches the upper bound for any fixed
k. A simple near-optimal algorithm for computing
the illuminated region is presented, which runs
in O(n2k log n) time and O(n2k
) space for k > 1, and in O(n2 log2
n) time and O(n2 ) space for k
= 1. |

|
|
Counting
triangle crossings and halving planes
T. K. Dey and H.
Edelsbrunner.Invited paper in a special
issue, Discrete & Computational Geometry,
Vol. 12 (1994), 281--289 Prelim.
version in SoCG 1995.
Every collection
of t > 2n^2 triangles with a total of
n vertices in R^3 has \Omega(t^4/n^6) crossing
pairs. This implies that one of their edges
meets \Omega(t^3/n^6) of the triangles. From
this it follows that n points in R^3 have only
O(n^{8/3}) halving planes.
Reprint available
upon request |

|
|
On
counting triangulations in d dimensions
T. K. Dey. Computational
Geometry: Theory and Applications, Vol. 3 (1993), 315--325.
Given a set of n labeled
points on S^d, how many combinatorially different geometric triangulations
for this point set are there? We show that the logarithm of this number
is at most some positive constant times n^{\floor d/2}+1. Evidence is provided
that for even dimensions d the bound can be improved to some constant times
n^{d/2}.
|
|
|